Table of Contents
Post model analysis
Dual analysis
T. Jansson
Constrained optimisation background
The supply model in CAPRI is a constrained optimization problem, maximizing profits plus a nonlinear term subject to multiple constraints. In some simulations, production activities in the model are affected in several ways simultaneously, and it is difficult to understand what the key drivers are behind a specific change. There may be changes both in parameters of the model such as prices or subsidies and also of dual values of resources such as land or fodder. Then a dual analysis can help you decompose the impacts by explaining how much the profitability of a production activity changed due to various factors. The key idea is to analyse how each term of the first order conditions changed.
For any well-behaved optimization model (one that e.g. maximizes a concave objective function on a convex constraint set) we can formulate the first order condition stating that in the optimal point, the sum of all marginal changes of all variables would provoke no change1) in the objective function. Let \(i=1…n\) be activities in the model, \(x_i\) be the level of activity i, \( f:\mathbb{R} _n\rightarrow \mathbb{R}\) be the concave and continuously differentiable objective function (e.g. profits), and \( g_j:\mathbb{R} _n\rightarrow \mathbb{R}\) be a function serving as a restriction for each of \(j=1…m\) resources. Finally, assume that all activity levels have to be non-negative2). The agent of the model acts as if solving the following maximization problem:
\begin{equation*} max \, f (x_1,...,x_n) \end{equation*}
Subject to
\begin{align} \begin{split} \begin{matrix} g_j(x_1,...,x_n) = 0 & [\lambda_j] & \forall j= 1 ... m \\ x_1 \ge 0 & [\pi_i] & \forall i= 1 ... n \end{matrix} \end{split} \end{align}
Greek letters (λ and π) in square brackets denote the Lagrange multipliers associated with each constraint. The Lagrange function3) for this problem can be written
\begin{equation} L(x_1, ... ,x_n,\lambda_1, ... , \lambda_m,\pi_1, ... , \pi_n) = f(x_1, ... ,x_n) - \sum_j \lambda_j g_j(x_1, ... ,x_n) + \sum_i\pi_ix_i \end{equation}
The necessary conditions for an optimal solution include the first order derivative of the Lagrangean with respect to the activity levels:
\begin{equation} \frac{\partial L}{\partial x_i} = \frac{\partial f}{\partial x_i} - \sum_j \lambda_j \frac{\partial g_j}{\partial x_i} + \pi_i = 0 \end{equation}
The functions f and g depend on some parameters, e.g. prices and technical i/o coefficients respectively that were not shown in the exposition above in order to reduce the size of the expressions. By changing such parameters, we introduce shocks to the model. Assume that in a reference scenario, we have prices \(p^0\) and technology \(a^0\) resulting in the solution \( (x_1^0,…,x_n^0,λ_1^0,…,λ_m^0,π_1^0,…,π_n^0 ) \). In another simulation, we have other prices \(p^*\) and technology \(a^*\) resulting in the alternative solution \( (x_1^*,…,x_n^*,λ_1^*,…,λ_m^*,π_1^*,…,π_n^* )\).
In this simulation we now would like to know more about why some particular activity \(x_i\) reacts as it does, i.e. why \(x_i^*\) is different from \(x_i^0\). We then compute each term in the first order conditions, and compare the two simulation. To be slightly more explicit, we can assume that the resources are j={“land” ,“fodder” ,“young animals” }. We can then do a comparison such as the following:

If we would compute the difference between the two rows above for each corresponding term, the differences would also sum up to zero, and each difference would mean something and have a numerical value: The first term is the change in marginal profits, the second term is the change in marginal cost of land, the third is the marginal cost of fodder, the fourth the marginal cost of young animals, and the final term the possible marginal value of a lower bound on the activity at hand. This can usually be directly translated into a storyline, like “The price increase increases the marginal profit of barley production by q euro per hectare, which leads to an expansion of production until it is matched by a similarly large increase in land rents”.
Of course, each partial derivative may be further decomposed into its smallest parts. For instance, profits may contain several items such as revenues, costs and behavioural terms.
Example – removing greening payments and requirements
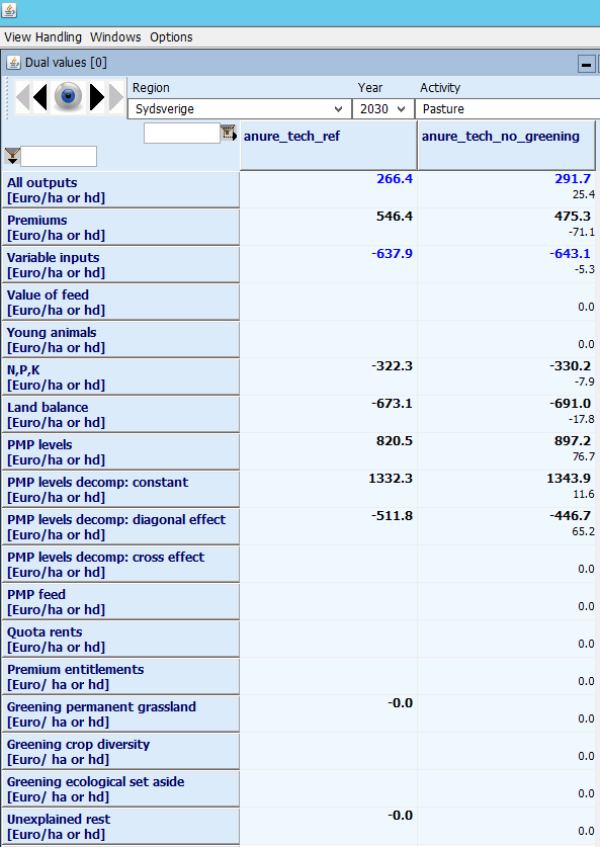
The dual analysis of the supply models is computed by a file called “supply/margcr.gms” (where margcr probably means “MARGinal Cost and Revenues”), which is always included after the last iteration. The figures below show the CAPRI GUI comparing the results of two scenarios: one reference continuing CAP after 2014 up to 2030, and a counterfactual where the greening payments and requirements are removed. We look at the results of a single region “Sydsverige” to avoid aggregation issues.
In Figure 39, we can look for the biggest changes (absolute difference between simulations is printed in brackets in the right hand column), and find a 71 euro reduction in payments. This is in line with the scenario, which removed 30% of the farm payment. All other positions adjust to some extent, and as usual with CAPRI, we find a similarly sized change in “PMP terms” (+77 euro income or reduction in costs), i.e. the behavioural terms adjust. As a note, we see that for this region, grassland is highly unprofitable in the reference scenario, and therefore the PMP term is calibrated to become a marginal income. The PMP effect is decomposed 4)into a change in the constant term (brought about by a shift between GRAI and GRAE), diagonal terms (the main effect, 65 euro) and cross effects (zero in this case).
Figure 38: Dual analysis of changes in pasture area (intensive and extensive) in a scenario removing the CAP greening components
There are more adjustments. Also land rents drop by 18 euro, the output of grass shown in the first line increases in value by 25 euro. Both variable costs and the value of the fertilizer restriction decrease, but those effects are comparatively minor.
Decomposition of changes in aggregates yields and activity related income indicators
The idea behind the decomposition is to analyze which factors drive the change in yields and income indicators using growth rates. Take for example the market income of cereals per ha at EU level. Its change in a simulation against the baseline depends on the change in prices and the change in yields. The change in yields in turns depends on the effect of the yield elasticity, the change in the shares of low and high technology variants, the change in the regional shares and, in weights of low and high yielding regions. And finally, the share of high and low yielding cereals such as soft what and rye in the total aggregate might change. When interpreting the results, it is often useful to understand the contribution of the different factors.
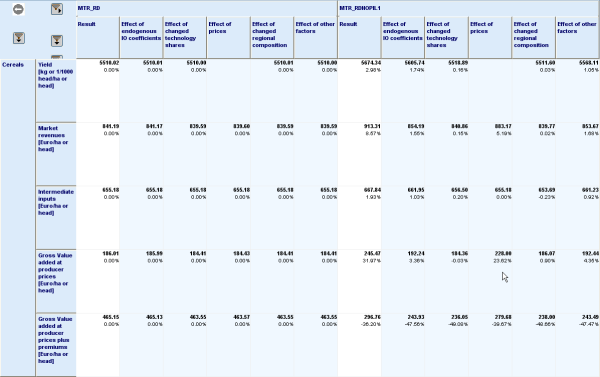
The screenshot below shows an example. All results shown are always expressed in the absolute value and the units used in the result set.
The columns are defined as follows:
- Result: Final result from the simulation – in the example below, average EU27 cereals yields increase by 8.57%.
- Effect of endogenous IO coefficients: Result calculated by using the final IO coefficients, but keeping all other factors (technology shares, prices, regional weights, activity levels) at trend levels – in the example below, market revenues per ha would have gone up by 1.55% if only the yields had adjusted.
- Effect of technology shares: Result calculated by only updating the technology shares, but keeping all other factors (IO coefficients, prices, regional weights, activity levels) at trend levels – in the example below, intermediate input costs would have increased by 0.2% of only the share of low and high yielding variants had changed.
- Effect of prices: Result calculated by only updating the prices shares, but keeping all other factors (IO coefficients, technology shares, regional weights, activity levels) at trend levels – in the example below, the Gross Value Added at producer prices would have increased by 23.62% if only the input and output prices had changed.
- Effect of regional composition: Result calculated by only updating the activity levels shares, but keeping all other factors (IO coefficients, technology shares, activity levels) at trend levels
- Effect of other factors: Difference between the start values and result, after all other effects above had been accounted for. Comprises the multiplicative cross-effects of the different effects, the effect of changed premiums in the case of the MGVA, and of change in the activity aggregate composition.
Figure 39: Illustrative scenario comparison for the yield and income indicator decomposition
It should be mentioned that the coding does not use information about potential changes of the premiums paid in scenario against the baseline, so that the results shown for the modified Gross Value Added should mainly show the different percentage changes on income once the level effect of the premiums is considered. The coding also stems from the time before climate related yield shock sceanrios or endogenous mitigation modelling. As the yield decomposition probably has not been regularly checked in this kind of scenarios, it is possible that some changes implemented in the CAPRI supply models need to be transferred to this reporting code to give reliable results in all kind of scenarios.
Post model sensitivity analysis with features in the supply model
The behaviour of the CAPRI supply model depends on the interaction between endogenous variables such as production and feeding activities both via the objective function and the constraints. Even if the dual analysis of the results may help, understanding the changes in levels of endogenous variables compared to the baseline is far from trivial. As the directions and size of certain impacts on the reported changes is not known, result analysis carries a high risk of mis-interpretations. A specific optional reporting tool has been developed therefore and is accessible though the CAPRI GUI (farm ⇒ supply model analysis) that systematically analyses the contributions of the different allocative mechanisms in the model. The basic idea consists in evaluating how the result at given prices would have looked like if certain endogenous model features would not have been used.
However due to various code changes in the last years it cannot guaranteed that the reporting option it still fully operational such that we refer the interested reader to earier versions of this documentation5).
Welfare analysis
A key element in analysing policy changes from an economic viewpoint is to look at welfare changes. The “classical” elements of a welfare analysis are changes in consumer and producer rents and for the tax payer. That concept is also followed in CAPRI.
For consumers, CAPRI uses the money metric concept. It can be broadly understood as a measurement for changes in the purchasing power of the consumer. The concept is also linked to the expenditure function as introduced in Section Behavioural equations for final demand:
\begin{equation} M(cpri^r,cpri^s,Y^r )=e(cpri^r,U(cpri^s,Y^r )) \end{equation}
Where e(.) is the expenditure function, \(Y^r\) is expenditure in the reference situation, and \(cpri^r (cpri^s)\) is the price vector in the reference (scenario) situation. The money metric is thus the expenditure the consumer would need at reference prices to be as well of as if facing the scenario prices at reference income. The difference of money metric for a given scenario to money metric in the reference situation is the equivalent variation. Considering the generalised Leontief form of the indirect utility function used in CAPRI (compare with Section Behavioural equations for final demand) we get
\begin{align} \begin{split} e (cpri^r, U(cpri^s,Y^r)) &= \left\{ F^r+ \frac{G^r}{G^s⁄(Y^r-F^s)}-Y^r \right\}+Y^r \\ & = \left\{ \frac {G^r}{G^s}(Y^r-F^s )-(Y^r-F^r ) \right\}+Y^r \end{split} \end{align}
The bracket {} is the equivalent variation of the change from the reference to the scenario situation. In the code (in gams/reports/welfare.gms) the momey metric is computed in a loop over products such that the contributions of single products are displayed6). It is also considered that the per capita demand needs to be multiplied with population.
For some agents the welfare accounting involves particularities for those regions covered by the regional programming models that will be discussed below. In the general case (for “non supply model regions”) producer welfare may be derived in the market model from the normalised profit function underlying the supply functions and the input demands for feed energy and land:
\begin{equation} \pi(p^s)=π_0+\sum_x as_x p_x^s+0.5 \sum_{x,y} bs_{x,y} p_x^s p_y^s \end{equation}
where \(p^s\) is the price vector in the scenario situation and the arbitrary constant \(\pi_0\) has been chosen as 50% of reference run revenues. In order to show the changes in producer welfare by product we compute producer welfare in the scenario as follows:
\begin{equation} \pi(p^s)-\pi(p^r)+\pi_0=\sum_x as_x(p_x^s-p_x^r)+0.5\sum_{x,y}bs_{x,y}(p_x^s p_y^s - p_x^r p_y^r )+\pi_0 \end{equation}
In the code (in gams/reports/welfare.gms) we are also considering that it is necessary to revert the normalisaiton of prices with the general price index
CAPRI uses the normalised quadratic form also for other agents, such that the calculation of welfare changes is very similar for
- the dairy industry (with margins adopting the role of prices)
- the processing industry (again with margins adopting the role of prices)
- the feed industry
Land supply is currently specified as responding to the log of land rents according to a land supply elasticity which also permits an easy calculation of land owner rent.
In the global market model, the main effects on taxpayer welfare comes through tariff revenues. Here it is also necessary to consider the allocation of TRQ rents, and if several bahavioural (“RMS”) regions are combined into a single market region (“RM”) then the tariff revenues of the market region need to be allocated.
For European (supply model) regions there are a number of particularities. First of all, CAPRI uses changes in the gross value added (GVA) plus premiums as the main indicator of producer (farmer) welfare. The gross value added is the difference between revenues (output quantities valued at farm gate prices) and intermediate input costs (input quantities with the exemption of the primary factors land, capital and labour multiplied with their farm gate prices). The GVA plus premiums is hence the sum the farming sector can spend to remunerate labour, capital and land, independent of property rights of these factors. GVA including subsidies is a traditional measure of “farm income” which has been one of the most important objectives of the CAP in the early years of CAPRI. It was considered useful therefore to monitor farm income defined in this way in the database and to compute it for scenarios. GVA plus premiums differs from some other income indicators
- “Farm profits” may be computed from GVA plus premiums considering ownership and some accounting rules for depreciation of capital, and family as well as non-family labour costs.
- “Economic profit” in the sence of the supply models would be the value of the supply model objective function which depends critically on the specification of unobserved cost function parameters (PMP).
- Farm household income would also consider non-farm income sources and income of all household members and therefore clearly differs from GVA.
Due to the allocation of output and input to individual activities, CAPRI allows to calculate the GVA for single production activities, and to aggregate it from there to groups of activities and over regions.
“Land owner welfare” and “feed industry welfare” are also treated differently as compared to non-European regions, in line with the supply model specification for land supply and feed use. Regarding “land owner welfare” the supply models specify costs for the supply of land to farming that may be interpreted as the opportunity costs of non-agricultural land use. Deducting this opportunity cost of land ensures that scenarios involving changes in land supply are not assessed in a biased way (e.g. by treating land as a “free” input without a price).
Feed demand is also reflected already in the supply models, in fact in a quite sophisticated manner, which balances not only for feed energy (as in the global market model) but also for protein. The GVA plus premiums therefore already includes the effects of changing feed costs and no additional calculation is needed.
The final particularity derives from the detailed representation of the CAP premium system in the supply models. For premium schemes, financing rates for the EU and national budgets as well as for pillar I and II of the CAP are defined, which allow to allocate costs to those different budgets. A few other CAP instruments have become largely irrelevant in the meantime, like the cost of public market “interventions” (purchases for storage at public cost), export subsidization and some subsidies paid for demanders of agricultural goods. These are also covered in the CAPRI welfare accounting (in case they would be revitalised).
Energy Use in Agriculture
Introduction and basics
The objective of the CAPRI energy indicator is to improve the existing CAPRI model in its capabilities to display environmental effects of agricultural production activities. In order to give a short overview of the structure of the energy indicator, the underlying methodology of Life Cycle Analysis will be introduced covering structure of the energy coefficients used for assessment. In a second part, the assessment methodology of the single direct and indirect components will be described. Finally, the structure of the results being processed by the energy module will be shown and hints for application will be given. Energy input quantification follows process analysis within the methodology description of Cumulative Energy Demand (KEA) guideline N° 4600 (VDI, 1997). Thereby, the KEA states the entire demand of non-renewable energy resources, valued as primary energy, which arises in connection with the production, use and disposal of an economic good (product or service) or which may be attributed respectively to it in a causal relation (VDI, 1997). A precise definition of balancing boundary setting is carried out according to local, temporal and technological criteria and is an important foundation for the KEA. Due to the high complexity and multiplicity of some of the interactions between individual processes, systematic delimitation frequently poses a central problem for energy analysis. A detailed determination of all relevant energy and material flows in the service life of a product requires a separation of the components of the KEA right down to the individual processes. An energy balance in this context registers energy quantities or energy types respectively in Joule or Watt-hours, crossing the defined balance space boundaries during the period of analysis. The energy balance boundaries are identical with the material balance boundaries (VDI, 1997). In the CAPRI context, the input part of the KEA concept is underlying the energy assessment of agricultural production. Life cycle analysis (LCA), by integrating the KEA concept offers a suitable framework for energy assessment of CAPRI production activities. Therefore, guidelines such as ISO 14040 and 14044 (DIN, 2006) are considered in the energy assessment process. Such procedure is based on process analysis, which can be defined as follows: “The network or processes required to make a final product are identified. Each input is assigned an energy requirement so that the total energy requirement can be summed” (Fluck, 1980). Setting the system borders precisely is an essential task in this concern. Figure 40 shows the relevant borders and integrated processes for CAPRI energy module. The term “Agricultural Production” in Figure 40 is the main interface between LCA and CAPRI production activities.
Figure 40: System border and processes considered for CAPRI energy input assessment
The connecting link between process-based material flows and the energy requirement analysis are energy content factors. Life cycle inventories of agricultural production systems are the necessary tool therefore. The role of inventories such as ecoinvent (2003) is to provide modules for infrastructure and inputs used in agricultural production necessary for modelling production systems. In the case of the CAPRI energy module, several aspects concerning inventories had to be considered. On the one hand, a broad range of different sources provide inventory databases designed for different countries in the agricultural context. On the other hand, to use a uniform methodological basis, a basic decision for inventories analysed by ecoinvent (2003) was taken. Firstly, a great number of single inventories (direct and indirect energy sources as well as agricultural processes such as drying or irrigation) had been analysed. Secondly, the inventories being used are updated regularly and by using SALCA061 (2006) database for CAPRI energy indicator, a most recent version of the inventories was used. Thirdly, special analysis for the CAPRI energy module such as quantifying energy for stables for animal production activities was carried out using the underlying methodology of ecoinvent database in order to consider specifics of CAPRI. Nevertheless, the ecoinvent agricultural inventories have been compiled mainly in a Swiss context using background data of Swiss agriculture. In order to use these inventories for CAPRI, some adjustments have been made. Some minor differences in the energy assessment between CAPRI energy module and other literature sources cannot be avoided. The reason might be in the reference period of the data (most literature data is of some years age) or in the Swiss-based approach of the inventories.
Energy assessment in CAPRI
To integrate the methodology which is described in Chapter Delineation into CAPRI, two parts are required for each single energy input component: an activity-specific, regionalized consumption quantity and an equivalent assessment factor. The following chapters present both parts for each input component integrated into CAPRI.
Direct energy sources
Direct energy covers those energy sources that are consumed directly in the production process for the purpose of generation of usable energy (Werschnitzky et al. 1987). For diesel fuel, petrol, heating oil, electricity, gas, coal etc., the input quantities of each animal and plant production activity are calculated and afterwards assessed by energy content factors. The content factors are based on ecoinvent modules using SALCA061 database (2006). Table 30 shows the main direct energy sources used in CAPRI.
Table 30: Energy content factors for direct energy input
| Direct energy component | Cumulative energy demand | Unit |
|---|---|---|
| Diesel | 45.7 | MJ/l |
| Electricity (at grid) | 11.7 | MJ/kWh |
| Heating Gas (in industrial furnace) | 47.9 | MJ/m3 |
| Heating Oil (in industrial furnace) | 49.7 | MJ/l |
Diesel fuel
Among the direct energy sources in agriculture, diesel fuel is one of the most important. Due to the fact that CAPRI does not include consumption data of diesel fuel, the input quantity is calculated on an activity-based approach using normative data. Therefore, the German KTBL database (KTBL, 2004) is applied. This database offers consumption quantities on a standardized methodological basis for common crop production activities. Different parcel sizes ranging from 1 ha up to 80 ha-parcel and different soil qualities (light, medium, heavy) are additionally considered. To apply this range to CAPRI, the link between the European Soil Map and CAPRI was adapted. Using literature information, a classification of the different soil type classes into light/medium/heavy soils was done and linked to the diesel use database. Parcel size data, which were not available on a member states level, is estimated from EUROSTAT Farm Structure Survey (EU-FSS) data, parameter C-04 displaying numbers of field parcels per farm. To consider work steps in which diesel is used but that are not covered by the KTBL database, such as setup time of machinery, transport processes or feed preparation for animal feeding, additional consumption is charged. Furthermore, processes such as irrigation are considered in the diesel use. In order to link the estimations with national consumption statistics, a correction factor is established. A special focus is on the fuel consumption of grassland. On the one hand, consumption is yield-driven (high grass yield requires more cuttings per season), on the other hand the pasture share has an impact on the total quantity of diesel use. Both aspects are considered in the CAPRI energy module: a stepwise calculation depending on the yield level is carried out for the grassland that is mowed. The pasture share is indicated by national sources or UNFCCC. Minor amounts of diesel fuel are used if irrigation is applied, such consumption is charged to the activity being irrigated.
Electricity
Electricity consumption plays a major role in animal production activities and drying cereals. Like diesel, data on electricity use is not included in CAPRI. Therefore a normative approach has been chosen to quantify consumption levels. Concerning housing systems, a distinction between the different activities has been made as well as a grouping of the EU countries in “North”, “Middle” and “South” to reflect the different requirements for heating and cooling. Charges in electricity use then have been set activity-specific and to a minor extent, depending on the herd sizes. Those charges are calculated on an animal-place basis. Electricity requirements for milk cooling are based on the CAPRI milk yield. Consumption quantities are taken from literature sources and calculations of Agroscope ART in Swit-zerland (Project BW04). Electricity used in grain drying is based on a normative approach due to lack of data of drying systems in the EU. Nevertheless, consumption quantities for drying are linked to the harvest moisture content as described in Chapter 7.5.2.11 
Heating oil and heating gas
Main consumption sources for heating oil and heating gas are greenhouses and grain drying. Greenhouses consumption quantity is taken from member states statistics, where available. Alternatively, literature data including national information on heated greenhouses is considered. Grain drying process is displayed, as mentioned for electricity, based on a normative approach.
Indirect energy sources
Indirect energy use describes external primary energy expenditures linked to materials utilised in production systems, balanced up to a defined system border (Diepenbrock, 1995; Moerschner, 2000). CAPRI energy indicator covers all relevant indirect energy sources. As for direct energy components, energy content data stem entirely from Ecoinvent modules using SALCA061 database (2006) to ensure a uniform assessment. The database for the most important indirect energy sources can be seen in Table 31. The following chapters give an overview on the methodology to estimate indirect components.
Table 31: Energy content factors for indirect energy input
| Indirect energy source | Cumulative energy demand | Unit |
|---|---|---|
| Tractor | 52.34 | MJ/kg machinery weight |
| Harvester | 49.27 | MJ/kg machinery weight |
| Trailed Machinery | 36.44 | MJ/kg machinery weight |
| Nitrate fertiliser | 58.99 | MJ/kg nutrient |
| Phosphate fertiliser | 40.06 | MJ/kg nutrient |
| Potassium fertiliser | 9.25 | MJ/kg nutrient |
| Herbicides | 218.62 | MJ/kg active substance |
| Insecticides | 299.02 | MJ/kg active substance |
| Fungicides | 124.38 | MJ/kg active substance |
| Lubricants | 79.17 | MJ/kg |
| Minerals | 13.52 | MJ/kg |
| Salt | 6.62 | MJ/kg |
Mineral fertiliser
Mineral fertiliser energy assessment follows CAPRI-endogenous calculated fertiliser use. Thereby, the assessment is linked to net mineral fertiliser use. Such regionalized and activity-specific input quantities divided into the fertiliser groups (Nitrate, phosphate, potassium) are assessed by the energy content coefficients as shown in Table 31. Those are compiled using average registered consumption quantities of the single fertilisers on the market, which are broken down to their active substance content.
Machinery use and lubricants
Machinery energy assessment is sub-divided into different machinery classes such as tractor, harvester and trailed machinery as well as special machinery such as irrigation or drying machinery on the one hand. On the other hand, a distinction between the machinery itself and the efforts for repairing and maintanance is made. In consequence, machinery stock data is required for every region. Such is partially available via EUROSTAT Farm Structure Survey (EU-FSS) parameter K-01 to K-03. The gaps have been filled, if available, with regional and national statistics. Tractor statistics are mostly available divided into different engine power classes, which permits a more detailed assessment mechanism. Energy assessment is carried out related to the physical weight of the machinery. Therefore tractor stock in a region is assessed with an average weight depending on the engine power class and afterwards sum up on NUTS-II level. The distribution of the weight over the useful lifetime of the machine is adequately to economic depreciation mechanism. An average useful lifetime of 20 years is assumed. This calculation step leads to the total machinery weight per NUTS-II region and year. The distribution towards the activities is calculated on a normative approach. Similar to diesel use, KTBL offers a database on machinery use expressed in machinery hours per ha for each activity under defined soil and parcel size conditions. This database divides between tractor-based processes and harvesting. The result of this procedure, expressed in kg machinery weight per ha is assessed with the energy content data shown in Table 31. Repair covering all exchanges of spare parts such as wheels, gearboxes, etc. during the lifetime of the machinery. The coefficient is determined by the energy depreciation factor. An equal approach is chosen for harvesters, whereas combine harvester stock is assumed to be used in the CAPRI CERE aggregate, other harvester stock by SUGB, POTA and ROOF. All activities receive an extra charge of trailed machinery. Such is, due to lack of data, determined by the tractor weight as a basis for activity-based coefficients on trailed machinery use. Trailed machinery receives energy for depreciation and repair. Lubricants` use is linked to machinery use time on an activity-based approach. Energy content is an average of different lubricants being used (such as engine oil, hydraulic oil, gearbox oil etc.).
Buildings energy use
Quantifying buildings energy use on a regional scale is rather difficult task due to lack of data. None of the common database offers any statistics on the amount, age or structure of agricultural buildings. Those few member states offering such data on a national level do not provide a standardised methodology. In consequence a normative approach has been chosen for CAPRI energy indicator. This approach is based on a life cycle analysis study carried out at AGROSCOPE ART (Project BW04). Standardized building types for different animal production activities have been set up using architectural planning instruments (“ART Preisbaukasten”) that permits quantifying the building material used and carrying out energy assessment. This data was broken down on a MegaJoule per square meter and year-term, whereas differentiation between depreciation, repair and maintenance and direct energy requirements was undertaken. Furthermore, several manure management systems are considered which permits using UNFCCC data on manure management (to be found in Table 4, UNFCCC “N2O Emissions from Manure Management”) for the different NUTS-0 regions and the most important animal production activities. Finally, to take use of EU-FSS herd size distribution data on NUTS-II, energy for buildings is calculated for different herd sizes. Depreciation of buildings energy is carried out following an economic depreciation approach whereas a useful lifetime of the building of 50 years is assumed. Depreciation covers efforts for building construction and waste disposal. Those parts of the building which have shorter useful lifetime, the exchange of spare parts and facilities as well as the waste disposal for such material is charged in the repair factor. The space charged for animals covers the entire stable area excluding space for feeding stuff. Pure animal space follows Swiss minimal space requirement regulations. To consider different building requirements between the regions of the EU, three region aggre-gates (North, Middle, South) are set up. For the set “South”, a typical Italian stable for cattle has been calculated. The charge for “Middle” is calculated based on Swiss stable systems, whereas “North” receives extra charges for heating. Due to lack of data for HENS and POUF, a pig breeding stable containing poultry-specific place requirements is taken for the calculations. Storage facilities for feeding stuff is charged depending on the input quantity of the relevant feeding stuff component, whereas a drive-in silo is the main type of storage facility. Such is charged for MAIF, GRAS and OFAR. Ma-chinery storage in barns is charged depending on the machinery size, derived from the engine power class, building type of the barn and a storage rate. Depreciation and repair distribution is equal to other building types.
Crop Protection
To reflect energy input via pesticides, the CAPRI-FADN data on monetary efforts for crop protection is used. Due to the fact that FAOSTAT offers consumption quantities of the different agents on a national level, a mechanism has been chosen to get those two parameters “quantities” and “energy content” together. Data from the EAA database helps to create the link in-between. Multiplying the quantities applied with the energy content data, the total sector energy consumption quantity can be calculated. Beside the pesticide categories shown in Table 31, growth regulatories are included in the calculation. Using the sector expenses, the “energy value” of plant protection application, expressed in MJ/€, is the basis for an activity-based assessment. The last step links the hectar-based CAPRI expenses for plant protection with the “energy value”. Certainly, this approach does not consider the shares of the different agents applied per activity, but taking the minor overall role of pesticides, it seems appropriate to follow the way described.
Seed
For considering seed in terms of energy, a distinction between certified and non-certified seed is done. A broad range of statistics, both on national and regional level indicate the share of certified and non-certified seed use. Information about total quantities applied is available for most CAPRI activities from literature. Non-certified as well as certified seed contain a “basic value” covering energy efforts for production of the output. Non-certified seed is being assumed to remain in the NUTS-II region for local production. Additionally to the basic value, energy efforts for cleaning, chemical treatment and storage are charged. Certified seed is charged, beside the basic value, with energy requirements for breeding, treatment, cleaning, packaging and transport.
Drying energy efforts
Energy required for drying mainly consists of two parameters: Firstly, the difference between harvest moisture content of the cereals and the marketable final moisture content and secondly the direct and indirect energy requirements for the reduction of one unit of moisture content. Estimation of harvest moisture content is carried out with the help of a regression model. To deliver explanatory variables, German harvest statistics are applied. In a first step a linear model is set up for each activity using climate data to find out an interrelationship between climate data and harvest moisture content. In a second step the linear models are applied for other EU countries using EU climate data to project harvest moisture content for regions where no harvest statistics are available.
Three different datasets are used for the generation of the projection module: Harvest statistics of Germany, Climate Data for the EU and Data about cereal cultivation regions in the EU:
- Harvest statistics of Germany: Data stem from a representative statistic survey of the years 2000, 2001 and 2002. Data is shown for 13 NUTS-I regions (excluding the city NUTS-I regions) and gives information about the weighted average moisture content of harvested cereals, divided into the activities wheat, rye, oats and barley.
- Climate data for the EU: Data stem from Climate Research Unit (CRU) of University of East Anglia in the version of CRU TS 2.1. Equally data from the years 2000, 2001 and 2002 is used. Addi-tionally long-term climate data is used displaying a 30-year average from the years 1961-1990.
- Cultivation Data for the EU: a dataset showing 0.5 x 0.5 degree grids with a cereal share lower than 10 % of UAA (based on CAPRI disaggregation crop data) was used to exclude grids being assumed irrelevant for the estimation process.
The harvest moisture statistical data and climate data was linked. The first step of the core statistic model was a principal component analysis (PCA), in which a broad range of variables were summarised into fewer principal components while preserving variability in the original variables. In the next step, the linear model was used to predict the average moisture content for regions, where no harvest moisture content data was available. Therefore, climate data as described above was used. Beside the exclusion of grid cells with a cereal area share lower than 10 percent of the UAA, a number of regions where grain drying is not applied, where not further considered. For the remaining regions, for each grid and production activity, a harvest moisture content estimate was calculated by the use of the linear models described above. In a fourth step, average harvest moisture content estimates are calculated by NUTS-I region and activity. Finally, the energy requirements for the reduction from the estimated moisture content to the marketable final moisture content was calculated.
Irrigation energy
Energy requirements for irrigation consist of direct and indirect components. Indirect requirements display machinery depreciation and repairs. EU-FSS (Parameter K-10) as well as national and re-gional sources indicate the share of mobile and fixed irrigation equipment. Furthermore, mainly national sources indicate share of surface and groundwater source of irrigation water. The irrigation machinery type is calculated based on Econinvent inventories. Depreciation and repair efforts are charged as described in Chapter 6.5.2.7 
Energy requirements for greenhouses
Energy consumption for greenhouses is determined by direct energy consumption for heating, supplementary illumination, disinfections of soil, substrate and drain water as well as minor efforts for buildings. Due to lack of data, barn energy requirements are charged. Direct energy sources are the main drivers for high total requirements. Concerning the area under glass, EU-FSS (Parameter D/15, D/17, G/07 and I/04) and several national institutions provide data, partially activity-based and mainly on NUTS-II level. For those regions where no model data was available, national institutions offered part of the data, whereas in some cases, no indication about activities was available. To distribute all available information and provide consistency as well as smooth greenhouses shares, a PMP term brings together the single components. Having set the share of each activity level under glass, the major part of energy consumption via greenhouses is calculated. Therefore, on the one hand, national consumption data is considered. This implies information on the activity-specific heated share of greenhouses, on consumption quantities of direct energy and on direct energy sources (heating gas, heating oil, coal, etc.). On the other hand, literature data is considered, where no national consumption statistics are available. Such methodology is only valid for Middle and Northern European countries, as, following literature, most greenhouses located in the Mediterranean basin could be considered as passive systems since they use very little external energy.
Feeding stuff
In animal production, feeding stuff plays a major role in energy consumption concerns. Quantification of the requirement is rather complex. The most important database are feeding coefficients implying quantities of different feeding stuff components on an activity- and regionalized basis. Furthermore, additional information on import shares, either on a national or on EU-level are required. Such coefficients are extracted from the CAPRI feeding module. Having those, the energy assessment is carried out. Taking basic ratio feed components (GRAS, MAIF, ROOF, OFAR), the following elements are charged: Firstly, production requirements are considered. Such cover all direct and indirect energy needs during the production process, divided by the yield. Secondly, processing efforts, such as storage and feed preparation are charged. Concerning grassland, pasture share is considered in the cal-culation process. Taking concentrates, things get a bit more complex. Those concentrates` components, that are produced in a NUTS-II region and consumed there are charged by the production requirements plus efforts for storage and processing (such as milling, mixing etc.). Those parts that stem from the relevant NUTS-0 region are furthermore charged with transportation needs. Finally, those parts of the ratio that are imported into the EU-27 receive a different treatment. Due to lack of methodological adequate assessed energy requirements of overseas production, an average of EU-27 production needs is assumed. Because data is not available or cannot be extracted in a meaningful way for some components (such as for soybeans), literature data are used. Then, overseas shipment is charged and the remaining processing efforts are considered as described above. Finally, feed supplements such as salt or minerals are charged taking animal-specific consumption quantities and energy content factors (Table 31).
Energy output assessment
In order to calculate energy balances or efficiency parameters, the output generated by agricultural production has to be assessed by its energy content. The CAPRI output level on the one hand is a basis for this assessment. Energy content factors, on the other hand, are used. Those are based on literature research. Basically, the assessment follows a caloric approach designed by FAO. Main coefficients are based on FAOSTAT data, some are taken from Mittenzwei (2006)
Energy allocation
For activities producing more than one marketable product (e.g. DCOW: COMI, BEEF, YCAM, YCAF), an allocation between the main output and the side-products has to be carried out. For plant production activities, no such allocation is done, the main product is charged with the complete energy needs. The allocation parameters assumed for animal production activities are shown in Table 32. The procedure follows literature data.
Young animals
To achieve a consistency in energy balances for animal activities, young animals assessment is an important item. To achieve such, all energy requirements necessary for a young animal are summed up following the lifelines within the young animal module of CAPRI. Nevertheless, an allocation of the energy content has to be carried out and follows allocation shares shown in Table 32.
Table 32: Allocation of animal products
| CAPRI activity | Main product share (%) | Side product N°1 share (%) | Side product N°2 share (%) | Side product N°3 share (%) | Side product N°4 share (%) |
|---|---|---|---|---|---|
| DCOW | COMI: 88 | BEEF: 8 | YCAM: 2 | YCAF: 2 | COMF: 0 |
| SCOW | YCAM: 44 | YCAF: 44 | BEEF: 8 | COMF: 4 | - |
| SOWS | YPIG: 100 | PORK: 0 | - | - | - |
| SHGM | SGMI: 50 | YLAM: 30 | SGMF: 10 | SGMT: 10 | - |
Analysis of CAPRI energy module results
The results of the CAPRI energy module can be displayed in various ways and on different levels. Table 33 gives an overview. Further down, each parameter is shown in more detail.
Table 33: Energy module results structure
| Parameter | Parameter Unit | Description | Availability |
|---|---|---|---|
| Energy per CAPRI activity unit | MJ/ha; MJ/head | Covers all energy requirements necessary for one CAPRI activity unit per year | Region-specific and activity-specific; weighted averages on NUTS-0 and EU level |
| Energy per CAPRI output unit | MJ/kg | All energy requirements for one CAPRI activity unit are divided by the output level; allocation between main product and by-products is carried out for a number of activities | Region-specific and activity-specific; weighted averages on NUTS-0 and EU level |
| Energy efficiency – Type “energy” | MJ/MJ | The output level of a CAPRI activity is assessed by its energy content (See Chapter 7.5.3) whereas allocation between main product and side-products is done for some activities. The result is divided by all energy requirements of the CAPRI activity unit. In short: Energy output (per kg) divided by energy input (per kg) | Region-specific and activity-specific; weighted averages on NUTS-0 and EU level |
| Energy efficiency – Type “Finance” | MJ/€ | The output level of a CAPRI activity is assessed by its energy content (See Chapter 7.5.3) whereas allocation between main product and side-products is done for some activities. The result is divided by the income for the activity. | Aggregated on NUTS-II, NUTS-0 and EU level |
| Energy balance | MJ | The output level of all CAPRI activities of a region are assessed by its energy contents (See Chapter 7.5.3  ) whereas allocation between main product and side-products is done for some activities and then sum up over the region. The input energy requirements for all CAPRI activities are multiplied with the relevant activity levels and then sum up over the region. The result shows energy requirements (INPUT) and energy output (OUTPUT). Imports and exports of energy can be shown separately. ) whereas allocation between main product and side-products is done for some activities and then sum up over the region. The input energy requirements for all CAPRI activities are multiplied with the relevant activity levels and then sum up over the region. The result shows energy requirements (INPUT) and energy output (OUTPUT). Imports and exports of energy can be shown separately. | Aggregated on EU level |
| Energy requirements-overview | MJ/ha; MJ/head | On an activity-based, regional level, the composition of total energy requirements can be shown on an aggregated level. | Region-specific and activity-specific; weighted averages on NUTS-0 level |
| Energy requirements-detail | MJ/ha; MJ/head | On an activity-based, regional level, the composition of total energy requirements can be shown on in detail. | Region-specific and activity-specific; weighted averages on NUTS-0 level |
| Energy input units | Input unit/ha; Input unit/head | On an activity-based, regional level, the composition of input units driving the energy needs can be shown in detail. | Region-specific and activity-specific; weighted averages on NUTS-0 level |
| Energy content products | MJ/kg product | On an activity-based level, the energy content for products can be shown; energy assessment of output is based on this parameter; Energy content is assumed being equal throughout all NUTS-II regions. | Activity-specific |
Source: CAPRI Modelling System
Application notice
Basically, the energy module is designed as post-model analysis. This implies, that the energy module can be run independently from the CAPRI core model. Nevertheless, a number of energy parameters depend on CAPRI data that changes depending on the scenario and the time under consideration. Consequently, the energy module has to be run each time changes in a scenario result table occur. Having set changes in any of the energy module`s files, the GAMS-file “enerind_bas” has to be run. To transfer such changes in the energy module to the scenario tables, the GAMS-file ”enerind_calc” has to be run in each scenario mode.
Structure of output tables
A broad range of output tables permits to display results of the energy indicator. Some of those are presented in this chapter. Figure 41 shows some examples for display modes of the energy indicator.
Figure 41: Energy parameters: examples for results displaying
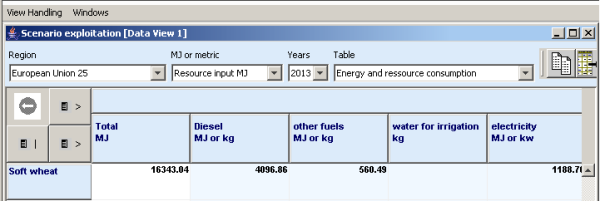
Example 1: Energy consumption - overview
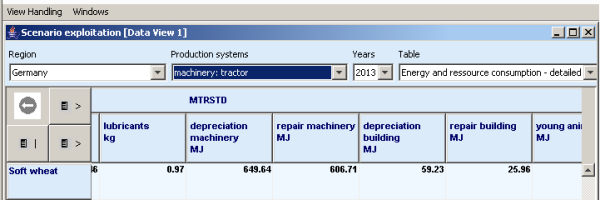
Example 2: Energy consumption - detailed
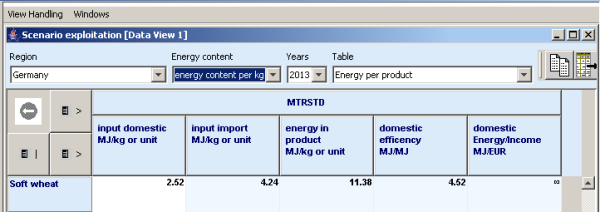
Example 3: Energy parameters with reference to the product
Example 4: Energy parameters: Sectoral balances ;Source: CAPRI Modelling System
Taking Example 1, the results of the energy consumption overview table are shown. This can be explored within the scenario exploitation table. Beside “Total MJ”, which indicates energy consumption per ha or head, a number of energy consumption categories such as diesel, electricity, machinery, fertiliser, young animals, seed and plant protection can be displayed either on a MJ basis or in metric units. Furthermore as can be seen in Example 2, detailed data on energy consumption can be displayed if required. Data on feeding stuff, housing systems, grassland use, tillage systems, machinery use, irrigation, greenhouse use, seed, plant protection, drying etc. can be shown activity- and region specific. Beside regarding the area or the animal, the product can be chosen as a reference point. As shown in Example 3, energy requirements per kg of product (expressed in MJ/kg) and domestic en-ergy efficiency (expressed in MJ/MJ) can be shown. On a sectoral basis, efficiency related to the in-come (expressed in MJ/€) is displayed. A sectoral balance can be extracted as shown in Example 4 summing up all energy requirements and all energy output.