Table of Contents
Input Allocation
The term input allocation describes how aggregate input demand (e.g. total anorganic N fertiliser use in Denmark) is ‘distributed’ to production activities. The resulting activity specific data are called input coefficients. They may either be measured in value (€/ha) or physical terms (kg/ha). The CAPRI data base uses physical terms and, where not available, input coefficient measured in constant prices.
Micro-economic theory of a profit maximising producer requires revenue exhaustion, i.e. marginal revenues must be equal to marginal costs simultaneously for all realised activities. The marginal physical input demand multiplied with the input price exhausts marginal revenues, leading to zero marginal profits. Marginal input demands per activity can only be used to define aggregate input demand if they are equal to average input demands. The latter is the case for the Leontief production function.
The advantage of assuming a Leontief technology in agricultural production analysis is the fact that an explicit link between production activities and total physical input use is introduced (e.g. environmental indicators can be linked directly to individual activities or activity specific income indicators, since gross margins can be calculated). The disadvantage is the rather rigid technology assumption. We would for example expect that increasing a crop share in a region will change the average soil quality the crop uses, which in turn should change yields and nutrient requirements. It should hence be understood that the Leontief assumption is an abstraction and simplification of the ‘real’ agricultural technology in a region. The assumption is somewhat relaxed in CAPRI as two ‘production intensities’ are introduced.
Input coefficients for different inputs are constructed in different ways which will be discussed in more detail in the following sections:
- For nitrate, phosphate and potash, nutrient balances are constructed so to take into account crop and manure nutrient content and observed fertiliser use, combined with gaseous losses. These balances ex post determine the effective input coefficients and regional availability of manure and overfertilisation parameters.
- For feed, the input calculation is rooted in a mix of engineering knowledge (requirement functions for animal activities, nutrient content of feeding stuff, recommendations on feed mix), observed data ex post (total national feed use, national feed costs), combined within a Highest Posterior Density (HPD) estimation framework.
- For the remaining inputs, estimation results from a FADN sample in the context of the CAPSTRAT project (2000-03) are combined with current aggregate national input demand reported in the EAA and standard gross margin estimations, again using a HPD estimation framework.
Input allocation excluding young animals, fertiliser and feed
There is a long history of allocating inputs to production activities in agricultural sector analysis, dating back to the days where I/O models and aggregate farm LPs where the only quantitative instruments available. In these models, the input coefficients represented a Leontief technology, which was put to work in the quantitative tools as well. However, input coefficients per activity do not necessary imply a Leontief technology. The allocated input demands can be seen as marginal ones (which are identical to average ones in the Leontief case) and are then compatible with flexible technologies as well.
Input coefficients can be put to work in a number of interesting fields. First of all, activity specific income indicators may be derived, which may facilitate analyzing results and may be used in turn to define sectoral income. Similarly, important environmental indicators are linked to input use and can hence be linked to activities as well with the help of input coefficients.
Given the importance or the input allocation, the CAP STRAT project (2000-2003) comprised an own work package to estimate input coefficients. On a first step, input coefficients were estimated using standard econometrics from single farm record as found in FADN. Additionally, tests for a more complex estimation framework building upon entropy techniques and integrating restrictions derived from cost minimization were run in parallel. The need to accommodate the estimation results with data from the EAA in order to ensure mutual compatibility between income indicators and input demand per activity and region on the one hand, and sectoral income indicators as well as sectoral input use on the other, requires deviating from the estimated mean of the coefficients estimated from single farm records. Further on, in some cases estimates revealed zero or negative input coefficients, which cannot be taken over. Accordingly, it was decided to set up a second stage estimation framework building upon the unrestricted estimates from FADN. The framework can be applied to years where no FADN data are available, and thus ensures that the results will be continuously used for the years ahead, before an update of the labor-intensive estimations is again necessary and feasible.
As a result of the unrestricted estimation based on FADN 1)a matrix of input coefficients for 11 input categories (Total Inputs, Crop Only Inputs, Animal Only Inputs, Seeds, Plant Protection, Fertilizer, Other Crop Inputs, Purchased and Non-Purchased Feeds and Other Animal Only Inputs) and their estimated standard errors is available. Some of those coefficients are related to the output of a certain activity (e.g. how much money is spend on a certain input to produce one unit of a product), some of them are related to the acreage of on activity (input costs per activity level).
All of the econometric coefficients were required to be transformed into an ‘activity level’ form, due to the fact that this is the definition used in the CAPRI model. Before this could be done, it seemed necessary to fill up the matrix of estimated coefficients because some estimates were missing and others were negative. In order to this we constructed a number of coefficients that were weighted averages among certain groups. These mean coefficients were the following.
- Mean coefficients of activity groups. Each activity was allocated to a certain group (e.g. soft wheat belonged to cereals). For each group we built weighted averages among the positive estimates within a group using the estimated t statistics as weights. This coefficient only existed if there was at least one positive estimate inside that group and was then used to replace the gaps inside the coefficient matrix. If that mean coefficient was not available, due to no positive estimate inside a group at all, the next type of mean coefficients became relevant:
- Mean coefficients for an activity among European regions. This second type of mean coefficients calculates weighted averages among three types of regional clusters. These clusters are Northern European States, Southern European states and all European regions. Again, the estimated t statistics were used as aggregation weights. Unfortunately, this type of averages did not fill all gaps in the coefficient matrix as there were some activities that had no positive estimate over the entire EU. For those the third type of mean coefficients was calculated.
- Mean coefficients for activity groups among regional clusters. Here we calculated for the three regional clusters the averages of the first type of mean coefficients. As even the latter are synthetic, we gave each mean of them the same weight. Fortunately there was only a small probability that this coefficient did not exist for one of the groups as this was only the case if no coefficient inside a group over the entire EU had a positive estimate, which was not the case.
Following these rules we finally got a matrix of estimated and synthetic calculated input coefficients for both, the ‘per activity level’ and the ‘per production’ unit definition2). For the synthetic one there was no estimated standard error available but we wanted to use those later on. So we assumed them –to reflect that these coefficients have only weak foundation– to have a t statistic of 0.5.
The ‘per level’ definition was only taken over if the coefficient was really estimated or if no per production unit definition did exist. To transfer the latter into per activity level definition, we multiplied them with the average yield (1985 2001) of the respective activity. The resulting coefficients and their standard errors were then used a HPD approach as a first set of priors3).
Missing econometric estimates and compatibility with EAA figures were not the only reasons that made a reconciliation of estimated inputs coefficients necessary. Moreover, the economic sense of the estimates could not be guaranteed and the definition of inputs in the estimation differed from the one used in CAPRI. Therefore we decided to include further prior information on input coefficients in agriculture. The second set of priors in the input reconciliation was therefore based on data from the EAA. Total costs of a certain input within an activity in a European Member State was calculated by multiplying the total expenditures on that input with the proportion of the total expected revenue of that activity to that of all activities using the input. Total expected revenue in this case was the production value (including market value and premiums) of the respective activity. If this resulted in a certain coefficient being calculated as zero due to missing data, then this coefficient would be replaced by one from a similar activity e.g. a zero coefficient for ‘MAIF’ would be replaced by the coefficient for ‘GRAS’
This kind of prior information tries to give the results a kind of economic sense. For the same reason the third type of priors was created based on standard gross margins for agricultural activities received from EUROSTAT. Those existed for nearly all activities. The set from 1994 was used, since this was the most complete available. Relative rather than absolute differences were important, given the requirement to conform to EAA values4).
Given the three types of prior information explained above –estimated input coefficients, data from EAA and standard gross margins , a HPD estimator has been used to reconcile the prior information on input coefficients. Accounting constraints ensure (see in “dist_input.gms”) first that gross margins for an activity is the difference between expected revenue per activity level of that activity and the sum over all inputs used in that activity and second that the sum over all activities of their activity levels multiplied with an input gives the total expenditures on that input given by the EAA. The estimation is carried out in GAMS within and run for each year in the database. Some bounds are further set to avoid estimates running into implausible ranges.
The Highest Posterior Density estimation yields monetary input coefficients for the fertiliser types (Nitrate, Phosphate, Potassium), seeds, plant protection, feeds, pharmaceutical inputs, repairs, agricultural service input, energy and other inputs. While some of these can be directly used in the CAPRI model, we need special treatments for others –e.g. fertilisers, because they are used in physical units inside the model, and feeds, since they are much more disaggregated.
Input allocation for young animals and the herd flow model
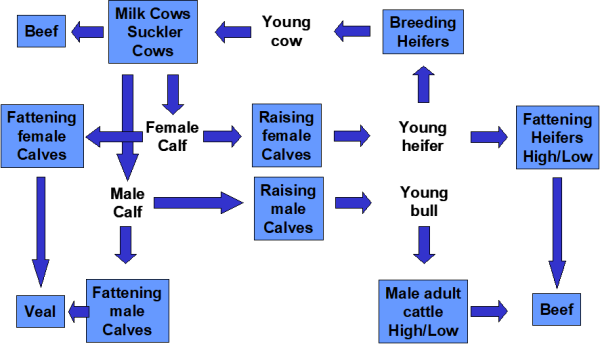
Figure below shows the different cattle activities and the related young animal products used in the model. Milk cows (DCOL, DCOH) and suckler cows (SCOW) produce male and female calves (YCAM, YCAF). The relation between male and female calves is estimated ex post in the COCO framework. These calves are assumed to weigh 50 kg at birth (see gams\feed\feed_decl.gms) and to be born on the 1st of January. They enter immediately the raising processes for male and female calves (CAMR, CAFR) which produce young heifers (YHEI, 300 kg live weight) and young bulls (YBUL, 335 kg). The raising processing are assumed to take one year, so that calves born in t enter the processes for male adult fattening (BULL, BULH), heifers fattening (HEIL, HEIH) or heifers raising (HEIR) on the 1st January of the next year t+1. The heifers raising process produces then the young cows which can be used for replacement or herd size increasing on the first of January of t+2. The table below the diagram shows a numerical example (for DK, 1999-2001) for these relationships.
Figure 5: The cattle chain
Source: CAPRI Modelling System
Accordingly, each raising and fattening process takes exactly one young animal on the input side. The raising processes produce exactly one animal on the output side which is one year older. The output of calves per cow, piglets per sow, lambs per mother sheep or mother goat is derived ex post, e.g. simultaneously from the number of cows in t-1, the number of slaughtered bulls and heifers and replaced in t+1 which determine the level of the raising processes in t and number of slaughtered calves in t. The herd flow models for pig, sheep and goat and poultry are similar, but less complex, as all interactions happen in the same year, and no specific raising processes are introduced.
Table 7: Example for the relation inside the cattle chain (Denmark, 1999-2001)
| 1999 | 2000 | 2001 | ||
|---|---|---|---|---|
| Male calves used in t and born in t | ||||
| DCOWLEVL | Number of dairy cows | 667,03 | 654,08 | 631,92 |
| DCOWYCAM | Number of male calves born per 1000 dairy cows | 420,72 | 438,62 | 438,26 |
| Number of males calves born from dairy cows | 280,63 | 286,89 | 276,95 | |
| SCOWLEVL | Number of suckler cows | 127,36 | 126,91 | 124,85 |
| SCOWYCAM | Number of male calves born per 1000 suckler cows | 420,72 | 411,83 | 401,61 |
| Number of male calves born from suckler cows | 53,58 | 52,27 | 50,14 | |
| Number of all male calves born | 334,22 | 339,16 | 327,09 | |
| GROFYCAM | Number of male calves produced | 334,21 | 339,16 | 327,09 |
| CAMFLEVL | Number of male calves fattened | 81,32 | 72,57 | 49,18 |
| CAMRLEVL | Activity level of the male calves raising process | 252,89 | 266,59 | 277,91 |
| Sum of processes using male calves | 334,21 | 339,16 | 327,09 | |
| GROFYCAM | Number of male calves used | 334,21 | 339,16 | 327,09 |
| Female calves used in t and born in t | ||||
| DCOWLEVL | Number of dairy cows | 667,03 | 654,08 | 631,92 |
| DCOWYCAF | Number of female calves born per 1000 dairy cows | 404,15 | 421,58 | 412,86 |
| Number of female calves born from dairy cows | 269,58 | 275,75 | 260,89 | |
| SCOWLEVL | Number of suckler cows | 127,36 | 126,91 | 124,85 |
| SCOWYCAF | Number of male calves born per 1000 suckler cows | 404,15 | 398,04 | 387,21 |
| Number of female calves born from suckler cows | 51,47 | 50,52 | 48,34 | |
| Number of all female calves born | 321,05 | 326,26 | 309,24 | |
| GROFYCAF | Number of female calves produced | 321,05 | 326,27 | 309,24 |
| CAFFLEVL | Number of female calves fattened | 26,64 | 28,74 | 18,39 |
| CAFRLEVL | Activity level of the female calves raising process | 294,41 | 297,53 | 290,85 |
| Female calves used in t and born in t | 321,05 | 326,27 | 309,24 | |
| GROFYCAF | Number of female calves used | 321,05 | 326,27 | 309,24 |
| Young bulls used in t and young bulls produced in t | ||||
| BULFLEVL | Activity level of the bull fattening process | 262,94 | 252,89 | 266,59 |
| GROFIBUL | Number of young bulls used | 262,94 | 252,89 | 266,59 |
| GROFYBUL | Number of young bulls raised from calvs | 252,89 | 266,59 | 277,91 |
| CAMRLEVL | Activity level of the male calves raising process | 252,89 | 266,59 | 277,91 |
| Heifers used in t and heifers produced in t | ||||
| HEIFLEVL | Activity level of the heifers fattening process | 64,36 | 67,25 | 68,12 |
| HEIRLEVL | Activity level of the heifers raising process | 235,45 | 227,16 | 229,4 |
| Sum of heifer processes | 299,81 | 294,41 | 297,52 | |
| GROFIHEI | Number of heifers used | 299,81 | 294,41 | 297,53 |
| GROFYHEI | Number of heifers raised from calves | 294,41 | 297,53 | 290,85 |
| CAFRLEVL | Activity level of the female calves raising process | 294,41 | 297,53 | 290,85 |
| Cows used in t and heifers produced in t | ||||
| DCOWLEVL | Number of dairy cows | 667,03 | 654,08 | 631,92 |
| DCOWICOW | Number of young cows needed per 1000 dairy cows | 332,01 | 332,5 | 327,52 |
| Sum of young cows needed for the dairy cow herd | 221,46 | 217,48 | 206,97 | |
| DCOWSLGH | Slaugthered dairy cows | 221,47 | 217,48 | 206,11 |
| SCOWLEVL | Number of suckler cows | 127,36 | 126,91 | 124,85 |
| SCOWICOW | Number of young cows needed per 1000 suckler cows | 332,01 | 332,48 | 327,52 |
| Sum of young cows needed for the suckler cow herd | 42,28 | 42,20 | 40,89 | |
| SCOWSLGH | Slaugthered suckler cows | 42,29 | 42,19 | 40,72 |
| Sum of slaughtered cows | 263,76 | 259,67 | 246,83 | |
| GROFICOW | Number of young cows used | 263,75 | 259,67 | 247,86 |
| Stock change in dairy cows | (DCOWLEVL(t+1)-DCOWLEVL(t) | -12,95 | -22,16 | |
| Stock change in suckler cows | (SCOWLEVL(t+1)-SCOWLEVL(t) | -0,45 | -2,06 | |
| Sum of stock changes in cows | -13,4 | -24,22 | ||
| Sum of slaughtered cows and stock change | 235,45 | |||
| GROFYCOW | Numer of heifers raised to young cows | 235,45 | 227,16 | 229,4 |
| HEIRLEVL | Activity level of the heifers raising process | 235,45 | 227,16 | 229,4 |
Source: CAPRI Modelling System
The table above is taken from the COCO data base. In some cases, regional statistical data or estimates for number of young animals per adult are available, but in most cases, all input and output coefficients relating to young animals are identical at regional and national level. Nevertheless, experiences with simulations during the first CAPRI project phase revealed that a fixed relationship between meat output and young animal need as expressed with on bull fattening process overestimates the rigidity of the technology in the cattle chain, where producers may react with changes in final weights to relative changes in output prices (meat) in relation to input prices (feed, young animals). A higher price for young animals will tend to increase final weights, as feed has become comparatively cheaper and vice versa. In order to introduce more flexibility in the system, the dairy cow, heifer and bull fattening processes are split up each in two processed as shown in the following table.
Table 8: Split up of cattle chain processes in different intensities
| Low intensity/final weight | High intensity/final weight | |
|---|---|---|
| Dairy cows (DCOW) | DCOL: 60% milk yield of average, variable inputs besides feed an young animals at 60% of average | DCOH: 140% milk yield of average, variable inputs besides feed an young animals at 140% of average |
| Bull fattening (BULF) | BULL: 20% lower meat output, variable inputs besides feed an young animals at 80% of average | BULH: 20% higher meat output, variable inputs besides feed an young animals at 120% of average |
| Heifers fattening (HEIF) | HEIL: 20% lower meat output, variable inputs besides feed an young animals at 80% of average | HEIH: 20% higher meat output, variable inputs besides feed an young animals at 120% of average |
Source: CAPRI Modelling System
Input allocation for feed
The input allocation for feed describes how much kg of certain feed categories (cereals, rich protein, rich energy, feed based on dairy products, other feed) or single feeding stuff (fodder maize, grass, fodder from arable land, straw, milk for feeding) are used per animal activity level5).
The input allocation for feed takes into account nutrient requirements of animals, building upon requirement functions. The input coefficients for feeding stuff shall hence ensure that energy, protein requirements, etc. cover the nutrient needs of the animals. Further on, ex post, they should be in line with regional fodder production and total feed demand statistics at national level, the latter stemming from market balances. And last but not least, the input coefficients together with feed prices should lead to reasonable feed cost for the activities.
Estimation of fodder prices
Since the last revision of the EAA, own produced fodder (grass, silage etc.) is valued in the EAA. Individual estimates are given for fodder maize and fodder root crops, but no break down is given for fodder on arable land and fodder produced as grassland as presented in the CAPRI data base. The difference between grass and arable land is introduced, as conversion of grass to arable land is forbidden under cross compliance conditions so that marginal values of grassland and arable land may be different.
The price attached to fodder should reflect both its nutritional content and the production costs at regional level. The entropy based estimation process tries to integrate both aspects.
The following equations are integrated in the estimator. Firstly, the regional prices for ‘grass’, ‘fodder on arable land’ and ‘straw’ (fint) multiplied with the fed quantities at regional level must exhaust the vale reported in the economic accounts, so that the EAA revenues attached to fodder are kept unchanged:
\begin{equation} \sum_{r,fint}\overline{FEDUSE}_{r,fint}PFOD_{r,fint} = \overline{EAAP}_{OFAR,MS}+\overline{EAAP}_{GRAS,MS} \end{equation}
Secondly, the Gross Value Added of the fodder activities is defined as the difference between main revenues (from main fodder yield), other revenues, and total input costs based on the input allocation for crops described above.
\begin{equation} GVAM_{r,fint} = \overline{YIELD}_{r,fint}PFOD_{r,fint}+\overline{OREV}_{r,fint}-\overline{TOIN}_{r,fint} \end{equation}
Other revenues may be from the nutrient value in crop residues. Next, an HDP objective is added which penalises deviations from the a priori mode.
The a priori mode for the prices of ‘grass’ and ‘other fodder on arable land’ are the EAAP values divided by total production volume which is by definition equal to feed use. The price of straw for feed use is expected to be at 1 % of the grass price.
Supports for Gross Value Added per activity are centred around 150 % of the value of total inputs as allocated by the rules and algorithm described above, with wide bounds.
Wide supports for the Gross Value Added of the fodder activities mirror the problem of finding good internal prices but also the dubious data quality both of fodder output as reported in statistics and the value attached to it in the EAA. The wide supports allow for negative Gross Value Added, which may certainly occur in certain years depending on realised yields. In order to exclude such estimation outcomes as far as possible an additional constraint is introduced:
\begin{equation} GVAM_{r,fint} \ge \overline{TOIN}_{r,fint}\overline {gvafac} \end{equation}
The parameter \(gvafac\) is initialised with zero so that first a solution is tried where all activities have positive GVAs. If infeasibilities arise, the factor is stepwise increased until feasibility is achieved, to ensure that estimated fodder prices are giving the minimal number of activities with negative Gross Value Addeds.
Calibration of the feed allocation
The allocation of feed to animal activities has been changed several times (like the fertiliser allocation). The most recent version has been developed 6) in the Stable Release 2 (in the following: “Star2”) project which will become also the standard version in the CAPRI trunk at the next opportunity.
General concept
In the “pre-Star2”7) implementation, based on the CAPRI model procedures, the objective in the data consolidation in tasks “build regional database” (capreg base year) and “baseline calibration supply” (capmod, baseline mode) is to cover the daily needs per animal with the available feed stuff (considering the daily feed intake capacity). In CAPRI most parameters determining the actual requirements of animals can be derived from statistics, e.g. milk yield, final live weight, daily gain, Apart from the uncertainty of statistical data, the calculated requirements can be seen as the “true” requirements in a country or region, as the differences between different animal nutrition literature sources are usually small. Nonetheless uncertainty in the data derived parameters can often lead to an over- or underestimation of the requirements in a range of 5-20% from the computed average need. This uncertainty may be taken into account when specifying the objective function for the required allocation model in a high posterior density (hpd) approach where the uncertainty on feeding requirements is expressed in terms of a standard deviation. This basic approach also underlies the “pre-star2” feed allocation. The pre-star2 feed calibration approach also considered two economic indicators that depend on the feed allocation:
- Feed costs and
- Gross margins, in particular the avoidance of negative gross margins 8)
These two criteria have been abandoned because technical plausibility was considered more important for the feed allocation than the derived value items. It may be argued that uncertainty in feed prices should not be transferred to the physical coefficients which is a consequence when considering both in the objective. Furthermore, the pmp approach of CAPRI has proven able to cope with negative margins even though it is admitted that they may not be entirely plausible.
In the pre-star2 CAPRI approach minimum and maximum bounds on specified feeding stuffs are specified to ensure technical plausibility, but to prevent infeasibilities they left considerable degrees of freedom. Additional hard constraints were for lysin and fiber contents of feed. However, a detailed analysis revealed that the purpose of these restrictions to ensure plausible feed ratios, for example regarding the relation of concentrate feed and roughage, was often missed. It has been decided therefore to skip these constraints.
The revised feed allocation methodology includes several new additional terms in its objective to capture technical plausibility beyond the animal requirements in terms of energy and protein and technical reproducibility of the calibration approach. These will be explained in more detail in the following sections.
Equations An overview of the equations used in the old and new feed allocation procedure is given in Table below. The objective function has changed significantly and more details on this will be discussed below. The equations ensuring consistency among production and consumption of feed, as well consistency across regional levels are unchanged.
Table 9: Equations used in old and new feed allocation routine
| equation | |||
|---|---|---|---|
| old | new | description | comment |
| hpdFeed_ | hpdFeed_ | objective function | changed significantly (see following section) |
| FEDUSE_ | FEDUSE_ | Balance for feeding stuff regional | needed to achieve consistency between produced feed and feed input to all animals and among regional layers |
| FEDUSEA_ | FEDUSEA_ | Aggregation to regional feed input coefficient to aggregate one | |
| FEDUSES_ | FEDUSES_ | Fixation for feeding stuff regional in calibration | |
| REQSE_ | REQSE_ | Requirements of animals written as equality | for energy ENNE and crude protein CRPR |
| REQSN_ | Requirements of animals written as in-equality | other requirements (lysine, dry matter and fibre) | |
| MINSHR_ | Maximum feed shares | Constraints on single feed stuff not used as hard bounds in new version | |
| MAXSHR_ | Minimum feed shares | Constraints on single feed stuff not used as hard bounds in new version | |
| CST_ | CST_ | Definition of feed cost from feed input coefficients and prices | Feed cost in new version only for monitoring, not in objective or constraints |
| MEANDEV_ | Definition of average deviation from requirements for all herds | oversupply by animal type was pulled against the mean oversupply. | |
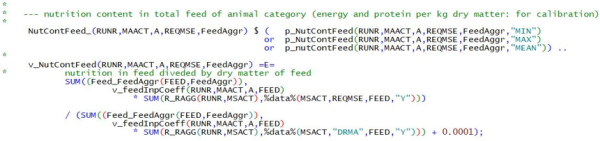
| NutContFeed_ | Nutrition content in the feed aggregates supplied to an animal category | nutrient content (per kg dry matter) is part of the objective | |
| FEDAGGR_ | aggregate to roughage, concentarte feed, etc | Defines feed aggregates from single bulks FEED | |
| FeedAggrShare_ | Calculate share of feed aggregates (roughage, concentrates, other) | shares of roughage and concentrate feed enter objective | |
| MeanFeedTotal_ | Calculates total feed intake in DM per animal | Part of revised objective function | |
The four additional equations developed in the new feed allocation procedure are described in more detail in the following.
For nutrient content (energy, crude protein) in the total feed mix or in concentrate feed recommendations are frequently given in the animal nutrition literature. The equation NutContFeed_ calculates this based on the estimated feed input coefficients and the data on nutrient content and dry matter per feeding stuff. A small number is added to the denominator to avoid division by zero (e.g. while gams is searching for a feasible solution)
FedAggr_
An aggregation of specific feeding stuff to aggregates (roughage, concentrates) is done since prior shares as well as minimum and maximum shares are more often found in the literature for aggregates than for single feedstuffs. The mapping is shown in Table below. It has been specified basically by putting into the “other” category all “special” items. Therefore, straw is a component of this “other” category rather than “roughage”.
Table 10: Mapping feeding stuff to feed aggregates
| FGRA | FMAI | FOFA | FROO | FCOM | FSGM | FSTR | FCER | FPRO | FENE | FMIL | FOTH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FeedRough | X | X | X | X | ||||||||
| FeedCons | X | X | X | X | ||||||||
| FeedOth | X | X | X | X | ||||||||
| FeedTotal | X | X | X | X | X | X | X | X | X | X | X | X |
One of the aggregates calculated is the total feed intake per animal. It is expected that, inspite of regional differences in fodder supply, this total feed intake is mostly a genetic characteristic of animals and hence should not vary markedly across regions. To influence this distribution in the objective, the average across regions needs to be computed.
Objective function
The objective function is extensively revised compared to the pre-star2 versions. The criteria to be optimised are now:
- coverage of animal requirements with feed
- regional variation of certain feed input coefficients
- concentration of energy and protein in feed mix
- shares of feed aggregates (roughage, concentrates, other) in total feed mix
- feed input coefficients of all FEED bulks receive prior expectations
The parameters in the objective function are partly means and imputed standard deviations AND so-called “soft” upper and lower limits. The “soft” limits increase the penalty significant when the solver picks values close to or even beyond them.
Coverage of animal requirements with feed

This part of the objective functions tries to minimize the difference between the requirements calculated from the feed input coefficients (v_animReq) and the expected (mean) requirements (p_animReq) coming from literature. Due to the weighting with number of animals (v_actLevl) and expected requirements (p_animReq) the optimal solution tends to distribute over or under supply of nutrients relatively even over all activities and regions. It has been decided to attach an exponent smaller one to these weights which strongly pulls them towards unity (see: […] 
Deviation of sub regional total feed intake from regional average

As argued above, we expect that total feed intake in DRMA is mostly a genetic characteristic of animals and hence should not vary markedly across regions. Deviations of (sub-)regional feed intake from the associated regional average (NUTS1 or MS) are therefore penalised.
Deviations of sub regional feed input coefficients of non-ruminants from regional average

As the comment explains, non-ruminants should have a rather standardised diet across regions.
Concentration of energy and protein in feed aggregates
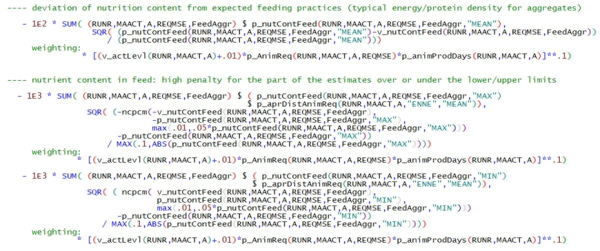
This part of the objective functions tries to minimize the difference between the nutrient content of feed aggregates (v_nutContFeed) and the expected nutrient (p_nutContFeed(…”MEAN”)) coming from literature or IFM-CAP. To avoid unreasonably large deviations from MEAN, lower and upper limits are introduced (MIN, MAX), where the penalty in the objective function increases significantly. The extra penalties rely on the GAMS built-in smooth approximation of the min operator (Chen-Mangasarian smoothing function ncpcm). The values for mean and upper and lower limits are presented in the table below.
Table 11: Expected nutrient content in total feed per animal category
| Energy | Crude protein | |||||
|---|---|---|---|---|---|---|
| MEAN | MIN | MAX | MEAN | MIN | MAX | |
| DCOL | 6.7 | 6.4 | 7 | 0.155 | 0.14 | 0.17 |
| DCOH | 6.8 | 6.6 | 7.2 | 0.155 | 0.14 | 0.17 |
| BULL | 6.7 | 6.2 | 7 | 0.155 | 0.14 | 0.17 |
| BULH | 6.8 | 6.4 | 7.2 | 0.155 | 0.14 | 0.17 |
| HEIL | 6.3 | 5.8 | 7 | 0.155 | 0.14 | 0.17 |
| HEIH | 6.8 | 6.2 | 7.2 | 0.155 | 0.14 | 0.17 |
| SCOW | 6.4 | 6 | 7 | 0.155 | 0.14 | 0.17 |
| HEIR | 6.4 | 6 | 7 | 0.155 | 0.14 | 0.17 |
| CAMF | 6.6 | 6.6 | 7.2 | 0.155 | 0.14 | 0.17 |
| CAFF | 6.6 | 6.6 | 7.2 | 0.155 | 0.14 | 0.17 |
| CAMR | 6.6 | 6.6 | 7.2 | 0.155 | 0.14 | 0.17 |
| CAFR | 6.6 | 6.6 | 7.2 | 0.155 | 0.14 | 0.17 |
| PIGF | 8 | 7.8 | 8.2 | 0.155 | 0.14 | 0.17 |
| SOWS | 8 | 7.8 | 8.2 | 0.155 | 0.14 | 0.17 |
| SHGM | 6.3 | 5.8 | 7 | 0.155 | 0.14 | 0.17 |
| SHGF | 6.3 | 5.8 | 7 | 0.155 | 0.14 | 0.17 |
| HENS | 8 | 7.8 | 8.2 | 0.18 | 0.14 | 0.2 |
| POUF | 8 | 7.8 | 8.2 | 0.18 | 0.14 | 0.2 |
Shares of feed aggregates in total feed intake in DRMA
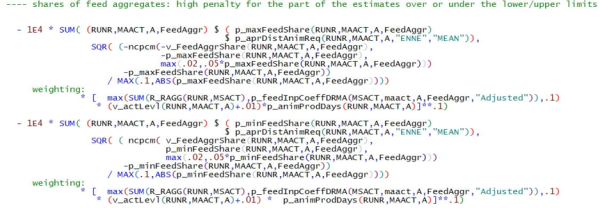
The shares of roughage and concentrate feed are only controlled by upper (p_maxFeedShare) and lower (p_minFeedShare) limits. The literature suggests that ruminants can digest at most 40% of concentrate feed (or at least 60% roughage), and perhaps 45% for activity DCOH. The upper and lower limits are partially taken from IFM-CAP, literature and expert knowledge of Markus Kempen (Assumed values in table 12).
Table 12: Maximum and minimum shares of feed aggregates
| Maximum shares | Minimum shares | |||
|---|---|---|---|---|
| FeedRough | FeedCons | FeedRough | FeedCons | |
| DCOL | 0.85 | 0.4 | 0.75 | 0.1 |
| DCOH | 0.7 | 0.45 | 0.6 | 0.1 |
| BULL | 0.8 | 0.4 | 0.65 | 0.1 |
| BULH | 0.8 | 0.4 | 0.65 | 0.1 |
| HEIL | 0.9 | 0.3 | 0.65 | 0.1 |
| HEIH | 0.9 | 0.3 | 0.7 | 0.1 |
| SCOW | 0.95 | 0.3 | 0.7 | 0.05 |
| HEIR | 0.9 | 0.3 | 0.7 | 0.05 |
| CAMF | 0.3 | 0.15 | ||
| CAFF | 0.3 | 0.15 | ||
| CAMR | 0.3 | 0.1 | ||
| CAFR | 0.3 | 0.1 | ||
| PIGF | 1 | 0.95 | ||
| SOWS | 1 | 0.9 | ||
| SHGM | 0.3 | 0.05 | ||
| SHGF | 0.3 | 0.05 | ||
| HENS | 0.99 | |||
| POUF | 0.99 | |||
For „other feed“ there are no lower bounds but rather low upper bounds: 10% for adult cattle, 5% for calves and sheep, 1% for pigs and 1E-6 (so near zero) for poultry.
Feed input coefficients for single feed bulks
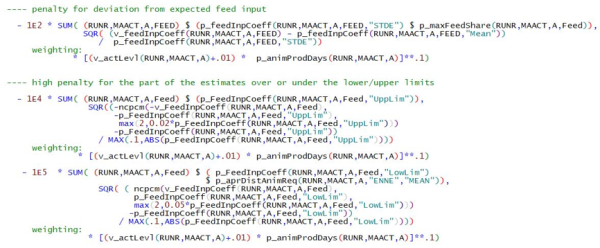
Apart from plausibility of the results a second objective of the revision has been reproducability. The previous specification essentially gave random results within the feasible set because no prior expectations had been specified. This has been revised with penalties for deviations of feed input coefficients from their assumed MEAN (specification to be explained below). However, just like is the case for the nutrient content of feed aggregates or their shares in the total, this prior information has to be considered quite imprecise which is reflected in rather low factors (1E2) attached to these terms. The penalties are increased if the solver tries to approach or exceed “soft” lower or upper limits. As the lower limits also turned out useful to prevent the solver from ending up in infeasible corners a higher factor has been attached to them (1E5).
It should also be reported that in many cases of infeasible solutions encountered in the extensive testing of this and previous specifications the last iteration result reported from the solver had often all feed input coefficients for some animal type zero or near zero. To avoid these cases the solution attempt starts with hard lower bounds:
In case of infeasibilities after x trials these are removed:
This procedure led to an acceptable or at least considerably improved stability of the feed calibration in tasks “build regional database” as well as “baseline calibration supply models”.
Priors for feed input coefficients
The priors for feed input coefficients are specified in a new include file capri\gams\feed\fedtrm_prior.gms:
The shares of feed aggregates in the diets of animal types may build upon recommendations from the literature (see the previous section). They are adjusted to be in line with the statistical ex post data or the baseline projections, giving the “adjusted” aggregate feed input coefficients shown in the code snippet above.
However, feed recommendations do snot exist for single feedstuffs because these are easily substitutable. Stability of the feed calibration requires however some priors. A simple default assumption made has been therefore: the composition of feed aggregates in terms of their components is the same for all animals (corresponding to the regional average). This is evidently a simplification such that the penalties for deviations from these priors have been set rather low to achieve both the desired stabilization effect while not competing too strongly with other components of the objective.
Nutrient contens and requirements
For the nutrient contents and requirement functions comparisons with IFM-CAP showed a good consistency such that the pre_star2 specifications were retained.
Calibration of PMP terms
The calibration of pmp terms for feeding coefficients is unchanged. But the constraints of minimum and maximum shares of feeding stuffs and some contents (fibre, lysin, etc) have been removed. The pmp terms have therefore a considerably increased role in simulations: Whereas the feed mix was so far steered by technical constraints, at least to a significant extent, all of these are gone except the equality constraints on feed energy and protein. The feed mix in simulation is therefore critically determined by the feed related pmp terms. In case of undesirable simulation behaviour it might be considered to include at least bounds for the total feed intake in terms of dry matter where feed recommendations apparently provide some bounds for plausible values.
Input allocation for fertilisers and nutrient balances
In the following section, the existing environmental indicators in CAPRI, planned and already achieved improvements, and possible further extensions are briefly discussed. It should be noted that CAPRI is basically a regionalised agricultural sector model, thus concentrating on the modelling of aggregated reactions of agricultural producers and consumers to changes in long term shifters as technical progress, income changes and CAP programs. Most indicators are rather robust pressure indicators and can be calculated easily based on fixed parameters approaches from the endogenous variables of the regional aggregate supply models. Accordingly, economic (dis)-incentives can be linked to the pressure indicators or further passive indicators can be introduced or the current ones changed easily.
Currently, CAPRI estimates the following environmental indicators:
- Greenhouse gas emissions from enteric fermentation (CH4), manure management (CH4, N2O), manure and mineral fertilizer application to soils (N2O, CO2), grazing animals (N2O), crop residdues (N2O), cultivation of histosols (N2O, CO2), indirect emissions from the volatilization of ammonia (N2O), indirect emissions from leaching and runoff (N2O), land use change emissions from carbon stock changes in above and below ground biomass (CO2), soils carbon stock changes (CO2,N2O), the burning of biomass (CH4,N2O). For details see (Pérez 2005) and Leip et al. (2010).
- Ammonia emissions from manure management, manure and mineral fertilizer application (Leip et al (2010).
- Nitrate Leaching and Runoff (Leip et.al. (2010)
- Soil erosion
Moreover, CAPRI provides the complete nutrient cycle for nitrogen and carbon, while for phosphate and potassium only the separate nutrient balances for crops and feed are considered. An important limitation of phosphate and potassium balancing is that output at tail is unrelated to feed intake because fixed coefficeints are used.
Nutrient balances for NPK and Nitrates Leaching
Nutrient balances in CAPRI are built around the following elements:
- Export of nutrient by harvested material per crop –depending on regional crop patterns and yields, and livestock products, and crop residues.
- Output of manure at tail –depending on animal type, regional animal population and animal yields, as final weights or milk yields (see section on Output at tail).
- Manure imports and exports (to the region)
- Input of mineral fertiliser –as given from national statistics at sectoral level.
- Input of crop residues, biological fixation, atmospheric deposition
- Emissions (NH3, NOx, N2, N2O, CO2, CH4, NO3, C from soil erosion) only for nitrogen and carbon, and removals (carbon sequestration) only for carbon
The numbers in the following table are based on older methodology and coefficients but nonetheless provide a useful illustration of the accounting. Details on the emissions are provided in the respective sections on ammonia and greenhouse gases. Details on the inputs in the sections on NPK output at tail and NPK input distribution.
Table 13: Nitrogen balance (EU 15, year 2001)
| INPUT | OUTPUT | ||||
| Import of nitrogen by anorganic fertiliser | a | 68.2 | Export of nitrogen with harvested material | f | 80.95 |
| Import of nitrogen by organic fertiliser (in manure) | b | 77.31 | Nitrogen in ammonia, NOx, N2O and runoff losses from manure fallen on grazings | g | 2.08 |
| Nitrogen from biological fixation* | c | 2.89 | Nitrogen in ammonia, NOx and N2O losses from manure in stable | h | 7.13 |
| Nitrogen from atmospheric deposition | d | 14.36 | Nitrogen in ammonia, NOx, N2O,N2 and runoff losses from manure storage | i | 2.53 |
| Nitrogen in ammonia, NOx, N2O and runoff losses from manure application on the field | j | 8.34 | |||
| Nitrogen in ammonia, NOx, N2O and runoff losses from organic fertiliser | k=g+h+i+j | 20.08 | |||
| Nitrogen in ammonia, NOx, N2O and runoff losses from mineral fertiliser | l | 2.89 | |||
| TOTAL INPUT | e=a+b+c+d | 162.768 | TOTAL OUTPUT | n=f+k+l+m | 103.92 |
| Nutrient losses at soil level (SURPLUS) | m=e-f-k-l | 58.85 | |||
The difference between nutrient inputs and outputs corresponds to the soil surplus. For nitrates the leaching is calculated as a fraction of the soil surplus, which is based on estimates from the MITERRA project, and depends on the soil type, the land use (grassland or cropland), the precipitation surplus, the average temperature and the carbon content in soils. For details see Velthof et al. 2007 “Development and application of the integrated nitrogen model MITERRA-EUROPE”. Alternatively, a version was developed which uses the leaching fractions from the official Greenhouse gas inventories of the member states. For phosphate, currently emissions (mainly superficial runoff) are not quantified.
NPK output at tail
The output of P and K at tail is estimated based on typical nutrient contents of manure:
Table 14: Nutrient content in manure in kg pure nutrient/m³
| P | K | |
| Cattle | 2.0 | 5.5 |
| Swine | 3.3 | 3.3 |
| Poultry | 6.3 | 5.1 |
These data are converted into typical pure nutrient emission at tail per day and kg live weight in order to apply them for the different type of animals. For cattle, it is assumed that one live stock unit (=500 kg) produces 18 m³ manure per year, so that the numbers in the table above are multiplied with 18 m³ and divided by (500 kg *365 days).
For the different types of cattle activities, it is hence necessary to determine the average live weight and the length of the production process.
For calves fattening (CAMF, CAFF), the carcass weight is divided by 60 % in order to arrive at final weight and a start weight of 50 kg is assumed. Daily weight increases are between 0.8 kg/day and 1.2 kg/day and depend proportionally on average stocking densities of cattle in relation to the average EU stocking density for which a daily weight increase of 1 kg/day is assumed. Total emissions per animal hence increase with final weights but decrease per kg of meat produced for intensive production systems with high daily weight increases. The same relationship holds for all other animal categories discussed in the following paragraphs.
For calves raising (CAMR, CAFR), two periods are distinguished. From 50 to 150 kg, a daily increase of 0.8 kg/day is assumed. The remaining period captures the growth from 151 to 335 kg for male and 330 kg for female calves, where the daily increase is between 1 kg/day and 1.4 kg/day, again depending on stocking densities.
The bull fattening process captures the period from 335 kg live weight to final weight. Daily increases are between 0.8 kg/day up to 1.4 kg/day, depending on final weights and stocking densities. Carcass weights as reported in the data base are re-converted into live weight assuming a factor of 54% for low and 57% for higher final weights.
The heifers fattening process captures the period from 300 kg live weight to final weight, assuming a daily increase of 0.8 kg/day. Carcass weights, as reported in the data base, are re converted into live weight assuming a factor of 54 % for low and 57 % for higher final weights.
Suckler cows are assumed to be whole year long in production and weight 550 kg, whereas milk cows are assumed to have a weight of 600 kg and are again for 365 days in production. Additional data relate to the additional NPK output per kg milk produced by cows and are taken from the RAUMIS model:
Table 15: Additional emission of NPK per kg of milk produced
| N | 0.0084 |
| P | 0.004 |
| K | 0.0047 |

The factors shown above for pigs are converted into a per day and live weight factor for sows by assuming a production of 5 m³ of manure per sow (200 kg sow) and 15 piglets at 10 kg over a period of 42 days. Consequently, the manure output of sows varies in the model with the number of piglets produced.
For pig fattening processes, it is assumed that 1.9 m³ are produced per ‘standard’ pig with a final carcass weight of 90 kg at 78 % meat content, a starting weight of the fattening period of 20 kg (weight of the piglet), a production period of 143 days and 2.3 rounds per year. The actual factors used depend on tables relating the final weight to typical daily weight increases.
For poultry, it is assumed that 8 m³ of manure are produced by 100 laying hens, which are assumed to weigh 1.9 kg and stay for 365 days in production. For poultry fattening processes, a fattening period of 49 days to reach 1.9 kg is assumed.
For sheep and goat used for milk production or as mother animals, the cattle factors are applied by assuming a live weight of 57.5 kg and 365 days in production. For fattening processes, a daily increase of 200 kg and a meat content of 60 % of the carcass weight are assumed.
The nitrogen emission factors from animal activities are coupled to crude protein intake (IPCC 2006), and hence the requirement functions for animal activities according to a farm gate approach. According to the literature (Udersander et al. 1993), there is a relation of 1 to 6 between crude protein and N in feeding. By combining this information with N retention rates per animal activity (IPCC 2000, Table 4.15), manure production rates can be estimated (N intake minus N retention). A specific advantage of that approach is the fact that gross nutrient surplus is not longer depending on assumption on fodder yields and manure emissions factors. Changing the fodder yields in the combined farm-gate and soil-balance approach in CAPRI will change both nutrient retention in crops and nutrient deliveries from manure by the same values, leaving the balance unchanged.
Table 16: Crude protein intake, manure production and nitrogen retention per head (EU 15, year 2001)
| Crude protein | Nitrogen in manure | Nitrogen retention | |
| BULH | 1.7 | 83.8 | 0.07 |
| BULL | 1.4 | 31.7 | 0.07 |
| CAFF | 0.8 | 21.5 | 0.07 |
| CAFR | 0.9 | 38.4 | 0.07 |
| CAMF | 0.8 | 20.2 | 0.07 |
| CAMR | 0.9 | 38.6 | 0.07 |
| DCOH | 4.3 | 210.1 | 0.20 |
| DCOL | 2.7 | 129.4 | 0.20 |
| HEIH | 1.5 | 64.4 | 0.07 |
| HEIL | 1.2 | 20.6 | 0.07 |
| HEIR | 1.7 | 95.9 | 0.07 |
| HENS (1000 units) | 21.2 | 900.9 | 0.30 |
| PIGF | 0.4 | 7.0 | 0.30 |
| POUF (1000 units) | 7.6 | 52.9 | 0.30 |
| SHGM | 0.2 | 13.7 | 0.10 |
| SHGF | 0.1 | 2.0 | 0.10 |
| SOWS | 0.9 | 36.4 | 0.30 |
| SCOW | 1.5 | 87.2 | 0.07 |
Calibration of the input allocation of organic and inorganic NPK
The input allocation of organic and inorganic fertilizer determines how much NPK organic and inorganic fertiliser is applied per ha of a crop, simultaneously estimating the NPK availability in manure as well as parameters describing the degree of overfertilisation. Firstly, nutrient export by the harvested material is determined, based on the following factors:
Table 17: Exports of nutrients in kg per ton of yield or constant Euro revenues
| N | P | K | |
| Soft wheat | 20 | 8 | 6 |
| Durum wheat | 23 | 8 | 7 |
| Rye | 15 | 8 | 6 |
| Barley | 15 | 8 | 6 |
| Oats | 15.5 | 8 | 6 |
| Grain maize | 14 | 8 | 5 |
| Other cereals | 18 | 8 | 6 |
| Paddy rice | 22 | 7 | 24 |
| Straw | 6 | 3 | 18 |
| Potatoes | 3.5 | 1.4 | 6 |
| Sugar beet | 1.8 | 1.0 | 2.5 |
| Fodder root crops | 1.5 | 0.09 | 5.0 |
| Pulses | 4.1 | 1.2 | 1.4 |
| Rape seed | 33 | 18 | 10 |
| Sunflower seed | 28 | 16 | 24 |
| Soya | 58 | 16 | 24 |
| Other oil seeds | 30 | 16 | 16 |
| Textile crops | 3 | 8 | 15 |
| Gras | 5 | 1.5 | 3.5 |
| Fodder maize | 3.2 | 2.0 | 4.4 |
| Other fodder from arable land | 5.5 | 1.75 | 3.75 |
| Tomatoes | 2.0 | 0.7 | 0.6 |
| Other vegetables | 2.0 | 0.7 | 0.6 |
| Apples, pear and peaches | 1.1 | 0.3 | 1.6 |
| Citrus fruit | 2.0 | 0.4 | 1.6 |
| Other fruits | 2.0 | 0.4 | 1.7 |
| Nurseries, flowers, other crops, other industrial crops | 65 | 22 | 20 |
| Olive oil | 4.5 | 1.0 | 0.5 |
| Table olives | 22.5 | 5.0 | 2.5 |
| Table grapes | 1.9 | 1.0 | 3.1 |
| Table wine, other wine | 1.9/0.65 | 1.0/0.65 | 3.1/0.65 |
| Tobacco | 30.0 | 4.0 | 45.0 |
The factors above are applied to the expected yields for the different crops constructed with the Hodrick Prescott filter explained above. Multiplied with crop areas, they provide an estimate of total nutrient export at national and regional level (right hand side of the figure below). The maximum exports per ha allowed are 200 kg of N, 160 kg of P and 140 kg of K per ha.
Ex post, the amount of nutrients found as input in the national nutrient balance is hence ‘known’ as the sum of the estimated nutrient content in manure plus the amount of inorganic fertiliser applied, which is based on data of the European Fertiliser Manufacturer’s Association as published by FAOSTAT. In order to reduce the effect of yearly changes in fertilizer stocks, three year averages are defined for the NPK quantities demanded by agriculture.
For the nitrogen balance, losses of NH3, N2O, NOx, N2 are handled as in MITERRA-Europe. The remaining loss to the soil, after acknowledging surface run-off, is disaggregated with leaching fractions into leaching or denitrification in soil. Atmospheric sources of N are taken into account as well (for details see section on nutrient balances).
Figure below offers a graphical representation of these relationships.
Figure 6. Ex-post calibration of NPK balances and the ammonia module
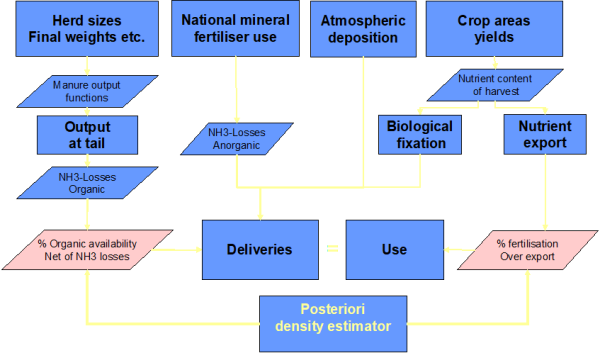
Source: CAPRI modelling system
The following equations comprise together the cross-entropy estimator for the NPK (Fnut=N, P or K) balancing problem. Firstly, the purchases (NETTRD) of anorganic fertiliser for the regions must add up to the given inorganic fertiliser purchases at Member State level:
\begin{equation} \overline{Nettrd}_{MS}^{Fnut}=\sum_r Nettrd_r^{Fnut} \end{equation}
The crop need –minus biological fixation for pulses– multiplied with a factor describing fertilisation beyond exports must be covered by:
- inorganic fertiliser, corrected by ammonia losses during application in case of N,
- atmospheric deposition, taking into account a crop specific loss factor in form of ammonia, and
- nutrient content in manure, corrected by ammonia losses in case of N, and a specific availability factor.

The factor for biological fixation (\(NFact^{biofix}\)) is defined relative to nutrient export, assuming deliveries of 75 % for pulses (PULS), 10 % for other fodder from arable land (OFAR) and 5 % for grassland (GRAE, GRAI).
The factor describing ‘luxury’ consumption of fertiliser (NutFac) and the availability factors for nutrient in manure (NavFac) are estimated based on the HPD Estimator:
\begin{align} \begin{split} min \; HDP &-\sum_{r,fnut} \left(\ \frac{NutFac_{r,fnut}-\mu_{r,fnut}^{NutFac}}{\sigma_{r,fnut}^{NutFac}}\right)^2\ \\ &-\sum_{r,fnut} \left(\ \frac{NavFac_{r,fnut}-\mu_{r,fnut}^{NavFac}}{\sigma_{r,fnut}^{NavFac}}\right)^2\ \\ &-\sum_{r,fnut} \left(\ \frac{NutFacG_{r,fnut}-\mu_{r,fnut}^{NutFacG}}{\sigma_{r,fnut}^{NutFac}}\right)^2\ \\ &-\sum_{r,ngrp} \left(\ \frac{Nitm{r,ngrp}-\mu_{r,ngrp}^{Nitm}}{\sigma_{r,fnut}^{NavFac}}\right)^2\ \frac{\overline {LEVL}_{r,UAAR}}{\overline {LEVL}_{r,ngrp}} \\ \end{split} \end{align}
The expected means \( \gamma\) for the availability for P and K in manure (Navfac) are centred around 50 %, for N at 50 %*40 %+25 %*86%, since 50 % are assumed to be released immediately, of which 60 % are lost as ammonia and 25 % are released slowly, with a crop availability of 86 %. These expected means at national level are multiplied with the regional output of the nutrient per hectare divided by the national output of nutrient per hectare so that the a priori expectation are higher losses with higher stocking densities. The lower limits are almost at zero and the upper limits consequently at the unity. The standard deviation \( \sigma\) is calculated assuming a probability of 1% for a zero availability and 1% for an availability of 100%.
The expected mean \( \gamma\) for the factor describing over fertilisation practices (Nutfac) is centred around 120 %, with a 1% probability for 160 % and a 1 % probability for 80 % (support points) with define the standard deviation \( \sigma\). Upper and lower limits are at 500% and 5%, respectively. A second factor (Nutfacg) is only applied for grassland and other fodder from arable land and centred around zero, with expected mean of +10% and a 10% with probabilities of 1%. Bounds for the factor Nutfacg are at 0.5 and 2.5.
The last term relates to the distribution of organic N to the different group of crops. The distribution is needed for simulation runs with the biophysical model DNDC (Joint Research Center, Ispra, Italy) linked to CAPRI results in the context of the CAPRI-Dynaspat project.
It is important to note that the CAPRI approach leads to nutrient output coefficient at tail taking into account regional specifics of the production systems as final weight and even daily weight increase as well as stocking densities. Further on, an important difference compared to many detailed farm models is the fact that the nutrient input coefficients of the crops are at national level consistent with observed mineral fertiliser use.
The nutrient balances are constraints in the regional optimisation models, where all the manure must be spread, but mineral fertiliser can be bought at fixed prices in unlimited quantities. Losses can exceed the magnitude of the base year but are not allowed to fall below the base year value. The latter assumption could be replaced by a positive correlation between costs and nutrient availability of the manure spread. There is hence an endogenous cross effect between crops and animals via the nutrient balances.
The factors above together with the regional distribution of the national given inorganic fertiliser use are estimated over a time series. Trend lines are regressed though the resulting time series of manure availability factors of NPK and crop nutrient factors for NPK, and the resulting yearly rates of change are used in simulation to capture technical progress in fertiliser application. The following table shows a summary by highlighting which elements of the NPK are endogenous and exogenous during the allocation mechanism and during model simulations:
Table 18: Elements entering the of NPK balance ex-post and ex-ante
| Ex-post | Ex-ante |
| Given: -Herd sizes ⇒ Manure output -Crop areas and yields ⇒ Export with harvest -National anorganic application Estimated: -Regional anorganic application -Factor for Fertilization beyond N export -Manure availability | Model result: -Herd sizes ⇒ manure output -Crop areas and yields ⇒ Export with harvest -National and Regional anorganic application Given: -Factor for Fertilization beyond export (trended) -Manure availability (trended) |
A good overview on how the Nitrogen balances are constructed and can be used for analysis can be found in: Leip A., Britz W., de Vries W. and Weiss F. (2011): Farm, land, and soil nitrogen budgets for agriculture in Europe calculated with CAPRI, Environmental Pollution 159(11), 3243-3253 and Leip, A., Weiss, F. and Britz, W. (2011): Agri-Environmental Nitrogen Indicators for EU27, in: Flichman G. (ed.), Bio-Economic Models applied to Agricultural Systems, p. 109-124, Springer, Netherlands.
Update note
The overall N Balance calibration problem has been revised several times. For example, since 2007 it delivers estimates of the shares of different sources of N (mineral fertiliser, excretions, crop residues) distinguished by crop groups. As of Stable Release 2.1, the calibration problem is augmented by an explicit maximization of the probability density functions described in the section on fertilization in the supply model chapter of this documentation 9).
The ammonia module
The ammonia (NH3) and nitrous oxide (NOx) output module takes the nitrogen output per animal from the existing CAPRI module and replaces the current fixed coefficient approach with uniform European factors per animal type by Member State specific ones, taking into account differences in application, storage and housing systems between the Member States. The general approach follows the work at IIASA and has been updated under the Ammonia project in 2006/07. The following diagram shows the NH3 sinks taken into account by coefficients.
Figure 7: Ammonia sinks in the Ammonia emission module
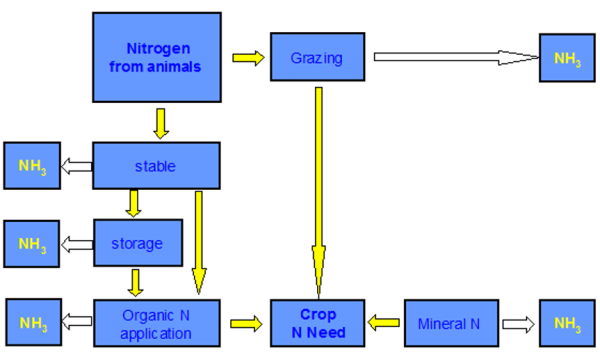
Source: CAPRI modelling system
In the figure above, white arrows represent ammonia losses and are based on uniform or Member State specific coefficients. A first Member State specific coefficient characterises for each animal type the share of time spent on grassland and spent in the stable. For dairy cows, for example, the factors are between 41 % spent in the stable in Ireland and 93 % in Switzerland. During grazing about 8% of the excreted N is assumed lost as ammonia.
The time spent in the stable is then split up in liquid and solid housing systems. To give an example, 100 % of the Dutch cows are assumed to use liquid manure systems, whereas in Finland 55 % of the cows are in solid systems. Ammonia losses in both systems are assumed to be identical per animal types but differ between animals. 10 % ammonia losses are assumed for sheep and goat, 12 % for cattle, 17 % for pigs and 20 % for poultry, if no abatement measures are taken.
The remaining nitrate is then either put into storage or directly applied to the ground. No storage is assumed for sheep and goats and in all remaining cases not-covered systems are assumed with loss factors of 4-20 % of the N brought initially into storage.
After storage, the remaining N is applied to the soil, either spread to the surface –losses at 8 40%% or using application techniques with lower (20-40% saving) or high (80% saving) emission reductions. According to IIASA data most farmers work still with the standard techniques.
The update of this calculation during the Ammonia project in 2006/07 has included new coefficients from IIASA through the project partner Alterra. Furthermore, it has been acknowledged that in addition to NH3 there are losses of N as N2O, NOx and N2. The loss factors depend on the application of abatement techniques the penetration of which may be varied in scenarios. Technically, the underlying calculations are embedded as GAMS code in an own module both called during updates of the data base and model runs. This module in turn includes GAMS code borrowed from the MITERRA-Europe model of our former partner.
Recently ammonia mitigation technologies have been implemented as endogenous farm practices (see section on greenhouse gases) and environmental constraints related to important environmental directives like the Nitrates Directive (ND), the National Emisssions Ceiling (NEC), and the Industrial Emissions Directice (IED) have been implemented directly to the supply model. For the ND we consider upper limits for the application of manure and total nitrogen, for the NEC the upper limits member states committed to until 2030, and for the IED minimum reqirements for the implementation of manure storage measures.
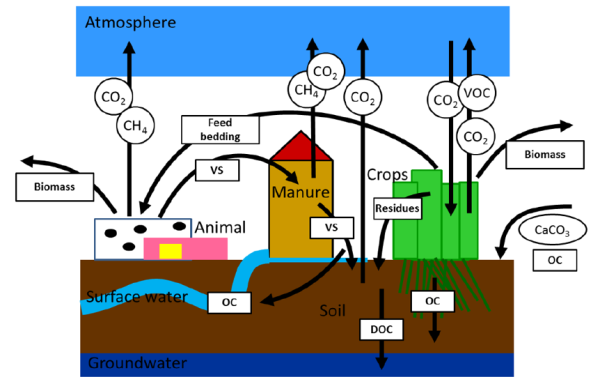
Carbon balance
The carbon cycle model quantifies relevant carbon flows in the agricultural production process related to both livestock and crop production (see Figure 6). Carbon flows and CO2 emissions from land use changes (LUC) are not considered meaning that the quantified balance applies to cropland remaining cropland and pasture/meadow land remaining in use. Default IPCC coefficients are used to quantify the carbon effects of LUC.
In CAPRI, so far the following carbon flows are taken into account, starting with animal production and ending with crop production (Weiss and Leip, 2016):
- Feed intake in livestock production (C)
- Carbon retention in livestock and animal products (C)
- Methane emissions from enteric fermentation in livestock production (CH4)
- Animal respiration in livestock production (CO2)
- Carbon excretion by livestock (C)
- Manure imports and exports to the region (C)
- Methane emissions from manure management in livestock production (CH4)
- Carbon dioxide emissions from manure management in livestock production (CO2)
- Runoff from housing and storage in livestock production (C)
- Manure input to soils from grazing animals and manure application (C)
- Carbon input from crop residues (C)
- Carbon export by crop products (C)
- Carbon dioxide emissions from the cultivation of organic soils (CO2)
- Carbon dioxide emissions from liming (CO2)
- Runoff from soils (C)
- Methane emissions from rice production (CH4)
- Carbon sequestration in soils (C)
- Carbon losses from soil erosion (C)
- Carbon dioxide emissions from soil and root respiration (CO2)
Accordingly, CAPRI does not consider the following carbon flows:
- Volatile organic carbon (VOC) losses from manure management (C)
- Carbon losses from leaching (C)
- Carbon dioxide emissions from urea application (CO2)
The VOC losses (non-CH4) from manure management are small and can be neglected. Carbon losses from leaching can be a substantial part of carbon losses from agricultural soils (see e.g. Kindler et al. 2011). Although they are not yet specifically quantified in the CAPRI approach, they are not neglected but put together with soil respiration in one residual value in the CAPRI carbon balance. CO2 emissions from urea application account for about 1% of total GHG emissions in the agriculture sector, but are not yet included in the CAPRI carbon cycle model.
Figure 8: Carbon flows in the agricultural production process
In the following, we briefly describe the general methodology for the quantification of the carbon flows that are taken into account in the CAPRI approach.
Subsequently, some details on the quantification of carbon flows (emissions and removals) are presented:
Feed intake in livestock production
Feed intake is determined endogenously in CAPRI based on nutrient and energy needs of livestock. The carbon content of feedstuff is derived from the combined information on carbon contents of amino acids and fatty acids, the shares of amino acids and fatty acids in crude protein and fats of different feedstuffs, and the respective shares of crude protein, fats and carbohydrates. For carbohydrates we assume a carbon content of 44%. Data was taken from Sauvant et al. (2004) and from NRC (2001).
Carbon retention in livestock and animal products
Similar to feed intake, we can quantify the carbon stored in living animals using the above mentioned data for animal products. At the end the values from meat are multiplied with the animal specific relation of live weight to carcass. For simplification, the fact that bones or skins etc. may have different carbon contents than meat is ignored.
Methane emissions from enteric fermentation
Methane emissions from enteric fermentation are calculated endogenously in CAPRI based on a Tier2 approach following the IPCC guidelines.
Animal respiration in livestock production
Intake of carbon is a source of energy for the animals. CAPRI calculates the gross energy intake on the basis of feed intake as described above. However, not all carbon is ‘digestible’ and hence can be transformed into biomass or respired. Digestibility of feed (for cattle activities) is calculated on the basis of the NRC (2001) methodology. Non-digestible energy (or carbon) is excreted in manure (see next point 5), while the ‘net energy intake’ refers to the equivalent to the energy stored in body tissue and products plus losses through respiration and methane.
According to Madsen et al. (2010) the heat production per litre of CO2 is 28 kJ for fat, 24 kJ for protein and 21 kJ for carbohydrates. Using a factor of 1.98 kg/m3 for CO2 (under normal pressure) or 505.82 l/kg we get 14.16 MJ/kg CO2 for fat, 12.14 MJ/kg CO2 for protein and 10.62 MJ/kg CO2 for carbohydrates, which translates into 0.071, 0.082 and 0.094 kg CO2 per MJ, respectively. These values are used to get the carbon directly from net energy intake (for each feedstuff), which is an endogenous variable in CAPRI depending on the feed intake. From this we subtract the carbon retained in living animals and in animal products and the methane emissions from enteric fermentation in order to compute the carbon respiration from livestock.
Carbon excretion by livestock
Carbon excretion is defined as the difference between the carbon intake via feed, the retention in livestock and the emissions as carbon dioxide (respiration) and methane (enteric fermentation):
\begin{equation} Excretion = Feed \; intake – retention – emissions (CO_2, CH_4) \end{equation}
Carbon excretion can, therefore, be determined as the balance between the positions 1-4. As Carbon retention plus emissions by default gives the net energy intake (see 4), this is equivalent to
\begin{equation} Excretion = C \; from \; gross \; energy \; intake – C \; in \; net \; energy \; intake \end{equation}
Manure imports and exports to the region
Manure available in a region may not just come from animal’s excretion in the region but could also be imported from other regions, while, conversely, manure excreted may be exported to another region. CAPRI calculates the net manure trade within regions of the same EU member state, and this has to be accounted in the carbon balance as a separate position. For simplification, the model assigns the emissions of all manure excreted to the exporting region, while the carbon and nutrients are assigned to the importing region.
Methane emissions from manure management in livestock production
Once the carbon is excreted in form of manure (faeces or urine), it will either end up in a storage system or it is directly deposited on soils by grazing animals. Depending on temperature and the type of storage, part of the carbon is emitted as methane. These emissions are quantified in CAPRI following a Tier 2 approach, using shares of grazing and storage systems from the GAINS database (for more explanation see also Leip et al. 2010).
Carbon dioxide emissions from manure management in livestock production
During storage or grazing, carbon is not only emitted in form of methane, but part of the organic material is mineralized and carbon released as carbon dioxide. Following the FarmAC model10), we assume a constant relation between carbon emitted as methane and total carbon emissions (methane plus carbon dioxide) of 63%. Therefore, the carbon loss through carbon dioxide emissions can be quantified as:
\begin{equation} C (CO_2) = C(CH_4) * 0.37/0.63 \end{equation}
Runoff from housing and storage in livestock production
Part of the carbon excreted by animals is lost via runoff during the phase of housing and storage. We assume the share to be equivalent to the share of nitrogen lost via runoff. In CAPRI we use the shares from the Miterra-Europe project, which are differentiated by NUTS 2 regions (for more information see Leip et al. 2010).
Manure input to soils from grazing animals and manure application
Carbon from manure excretion minus the emissions from manure management and runoff during housing and storage, corrected by the net import of manure to the region, is applied to soils or deposited by grazing animals. Other uses related to manure (e.g. trading, burning, etc.) are so far not considered in CAPRI. Moreover, we add here the carbon from straw from cereal production not fed to animals, assuming that all harvested straw (endogenous in CAPRI) not used as feedstuff is used for bedding in housing systems. The carbon content from straw is quantified in the same way as for feedstuff (see position 1). By contrast, other cop residues are treated under the position “carbon inputs from crop residues”. Bedding materials coming from other sectors are currently ignored.
Carbon input from crop residues
The dry matter from crop residues is quantified endogenously in CAPRI following the IPCC 2006 guidelines (crop specific factors for above and below ground residues related to the crop yield). For the carbon content, a unique factor of 40% is applied as the information used in position 1 (feed input) is generally only available for the commercially used part of the plants, but not specified for crop residues.
Carbon export by crop products
Carbon exports by crop products are calculated as described under position 1, using the composition of fat and proteins by fatty and amino acids and the respective shares of these basic nutrients in the dry matter of crops.
Carbon fixation via photosynthesis of plants
Photosynthesis is the major source of carbon for a farm. Carbon is incorporated in plant biomass as sugar and derived molecules to store solar energy. Some of these molecules are ‘exudated’ by the roots into the soil. They provide an energy source for the soil microorganism – in exchange to nutrients. In the current version of CARPI, we assume that 100% of the photosynthetic carbon not stored in harvested plant material or crop residues, returns ‘immediately’ to the atmosphere as CO2 (root respiration) and has therefore no climate relevance. Accordingly, the effective fixation of carbon via photosynthesis is assumed to equal the exported carbon with crop products plus the carbon from crop residues. It is, therefore, not calculated as an explicit term.
Carbon dioxide emissions from the cultivation of organic soils
Carbon dioxide emissions from the cultivation of organic soils are calculated by using shares of organic soils derived from agricultural land use maps for the year 2000. For details see Leip et al. (2010).
Carbon inputs from liming
Agricultural lime is a soil additive made from pulverised limestone or chalk, and it is applied on soils mainly to ameliorate soil acidity. Total liming application on agricultural land as well as the related emission factor is taken from past UNFCCC notifications. A coefficient per ha is computed dividing the UNFCCC total amount by the UAA in the CAPRI database. For projection purposes this coefficient per ha, computed from the most recent data, is maintained in simulations. In the context of the carbon balance the CO2 emissions are converted into C and become carbon input into the system.
Carbon runoff from soils
Similar to position 9 (runoff from housing and storage in livestock production) we assume that the share of carbon lost via runoff from soils is equivalent to the respective share of nitrogen lost. The respective shares are provided by the Miterra-Europe project (see Leip et al. 2010).
Methane emissions from rice production
Methane emissions from rice production are relevant only in a few European regions and they are quantified in CAPRI via a Tier 1 approach following IPCC 2006 guidelines.
Carbon sequestration in soils
Finally, we quantify the sequestered material after 20 years. The carbon change is based on simulations with the CENTURY agroecosystem model (Lugato et al. 2014) (aggregated from 1 km2 to NUTS2 level), and calculated from the difference in the manure and crop residue input to soils between the simulation year and the base year. This is done because carbon sequestration is only achieved from an increased carbon input, assuming that the carbon balance in the base year is already in equilibrium. The total cumulative carbon increase is divided by 20, in order to spread the effect over a standardised number of years (consistent with the 2006 IPCC guidelines).11)
Carbon losses from soil erosion
Carbon losses from soil erosion are calculated on the basis of the RUSLE equation (see the setion on soil erosion). In order to get the carbon loss we have to multiply with the carbon content of the soil. As approximation we assume a 3% humus share for arable land and a 6% humus share for grassland. The carbon share in humus is around 2/3.
Carbon dioxide emissions from respiration of carbon inputs to soils
Carbon losses from soil are quantified as the residual between all carbon inputs to soils, the emissions and the carbon sequestered in the soils:
\begin{align} \begin{split} &Carbon \; losses\; via\; soil\; and\; root\; respiration = \\ &Manure\; input\; from\; grazing\; and\; manure\; application \\ &+ input\; from\; crop\; residues \\ &- carbon \;losses \;(CH4)\; from \;rice\; production \\ &- carbon \;losses \;(CO2) \;from \;the \;cultivation\; of \;organic\; soils \\ &- carbon \;losses \;from \;runoff \;from \;soils \\ &- carbon \;losses\; from \;soil \;erosion \\ &- carbon \;sequestration \;in \;soils \\ \end{split} \end{align}
Carbon losses from leaching should also be subtracted, but they are not specifically quantified in the CAPRI carbon cycle model so far. Therefore, the share of soil respiration is currently overestimated by the model.
Greenhouse Gases
For the purpose of modelling GHG emissions from agriculture, a multi strategy approach is followed. It is important to take into account that agriculture is an important emitter of several climate relevant gases other than carbon dioxide. Therefore, three types of pollutants are modelled: methane (CH4) ,nitrous oxide (N2O), and carbon dioxide (CO2) emissions. The sources considered are: CH4 emissions from animal production, manure management and rice cultivation, N2O from agricultural soils and manure management, and CO2 emissions from agricultural soils. Moreover, carbon removals and emissions from land use change are quantified, and translated into CO2.
In CAPRI consistent GHG emission inventories for the European agricultural sector are constructed. As already mentioned, land use and nitrogen flows are estimated at a regional level. This is the main information needed to calculate the parameters included in the IPCC Good Practice Guidance (IPCC, 2006). The following table lists the emission sources modelled:
Table 19: Agricultural greenhouse gas emission sources included in the model
| Greenhouse Gas | Emission source | Code |
| Methane | Enteric fermentation | CH4Ent |
| Manure management | CH4Man | |
| Rice production | CH4Ric | |
| Land use change emissions from biomass burning | CH4bur | |
| Nitrous Oxide | Manure management | N2OMan |
| Manure excretion on grazings | N2OGra | |
| Application of synthetic fertiliser | N2OSyn | |
| Application of manure | N2OApp | |
| Crop residues | N2OCro | |
| Indirect emissions from ammonia losses | N2OAmm | |
| Indirect emissions from leaching and runoff | N2OLea | |
| Cultivation of histosols | N2Ohis | |
| Land use change emissions from the burning of biomass | N2Obur | |
| Carbon dioxide | Cultivation of histosols | CO2his |
| Applicaton of ureum | CO2urea | |
| Liming | CO2lim | |
| Land use change emissions from above and below ground biomass | CO2bio | |
| Land use change emissions from soil carbon changes | CO2soi |
For a detailed analysis of these single emission sources refer to Pérez 2006: Greenhouse Gases: Inventories, Abatement Costs and Markets for Emission Permits in European Agriculture -A Modelling Approach and Leip et al 2010: Evaluation of livestock sector’s contribution to the RU greenhouse gas emissions (GGELS).
The model code also comprises a life-cycle assessment for GHGs (first approach explained in Leip et al, 2010, but newer approach not yet documented in an official publication), and a module to estimate emission leakage in Non-European world regions (for details see e.g. Jansson et al.,2010: Estimation of Greenhouse Gas coefficients per commodity and world region to capture emission leakage in European Agriculture; Pérez Dominguez et al., 2012: Agricultural GHG emissions in the EU: An Exploratory Economic Assessment of Mitigation Policy Options., Van Doorslaer et al, 2015: An economic assessment of greenhouse gas mitigation options for EU agriculture). Moreover, in recent projects (Ecampa1-3) mitigation technologies and farm practices have been introduced to the supply model, which directly impact on the emissions. Currently, the following mitigation technologies can be activated:
- Anaerobic digestion
- Feed additives to reduce methane emissions from ruminants (lineseed, nitrate)
- Precision farming
- Variable Rate Technology
- Nitrification Inhibitors
- Better timing of fertilizer application
- Winter cover crops
- No Tillage
- Conservation Tillage
- Buffer strips
- Fallowing of histosols
- Measures to reduce methane emissions in rice production
- Increased legume share on temporary grassland
- Genetic measures to increase milk yields and feed efficiency
- Urea Substitution
- Manure application measures to reduce ammonia emissions (high and low efficiency)
- Manure storage measures to reduce ammonia emissions (high and low efficiency)
- Stable design measures to reduce ammonia emissions
- Low Nitrogen Feed
- Manure storage basins in concrete to reduce nitrate leaching
- Flexible limits for nitrogen application to soils
- Flexible limits for livestock density
- Vaccination against methanogenic bacteria
For details see Van Doorslaer et al. 2015, and Perez et.al 2016 (Most recent developments not yet published).
Soil erosion
Soil erosion is calculated on the basis of the RUSLE equation. The equation has the following form:
\begin{equation} A = R \cdot K \cdot L \cdot S \cdot C \cdot P \end{equation}
where
A = soil loss in ton per ha/acre per year
R = rainfall-runoff erosivity factor
K = soil erodibility factor
L = slope length factor
S = slope steepness factor
C = cover management factor
P = support practice factor
For more details on the factors used see Panagos et al. (2015).
Input allocation for labour
Labour (and other inputs) in CAPRI are estimated from a Farm Accounting Data Network (FADN) sample 12) and then these estimation results are combined with total labour requirements within a region (or aggregate national input demand reported in the EAA), using a Highest Posterior Density (HPD) estimation framework.
Labour Input Allocation
Input coefficients (family labour and paid labour, both in hours, as well as wage regressions for paid labour) were estimated using standard econometrics from single farm records as found in FADN. While many of results from this process are plausible a number of CAPRI estimates of labour input are inaccurate and untrustworthy, not least when fitted values for labour using the econometric coefficients are compared with total regional labour inputs recoverable from FADN data survey weights. To remedy this, a reconciliation process is undertaken to correct figures for labour input by adjusting the labour input coefficients for both total labour and family labour, handled in file gams\inputs\labour_calc.gms.
The reconciliation process has two components. The first component is to fix on a set of plausible estimates for the labour input coefficients (based on the econometric results) while the second involves a final reconciliation, where further adjustments are made to bring the estimates into line with the FADN values for labour inputs. Implementing these two steps involves the following procedures.
Step one involves preparing the econometric estimates in order to remove unreliable entries. This process removes specific unsuitable estimates for particular regions and crop types. In addition, this process also involves adjusting certain agricultural activities labour input coefficients (such as the estimates for triticale) so as to bring them into line with similar activities (such as for soft wheat). Furthermore, a Bayesian probability density function is used where EU averages are used as priors, and a number of bounds are added, in order to generate realistic labour input coefficients.
While the procedure described above help to ensure plausible estimates, the labour input values generated will still not be such as to reconcile total fitted labour with total actual labour at a regional or national level (as estimated by FADN). Step 2 in this process is to implement a final reconciliation, where the labour input coefficients are adjusted in order to bring estimates of labour input closer to the total labour used in the region/country. However, this adjustment process has to be balanced with a recognition that many of the labour input coefficient estimates are relatively reliable and that we don’t need or want to radically adjust all of them. Therefore the final reconciliation has to specify which input coefficients have to be adjusted most. The main way in which this is achieved is through the consideration of the coefficients’ standard errors in a second Bayesian posterior density function.
As well as the reconciliation process, two other procedures have to be carried out. The first results from the fact that a number of activities don’t have labour input coefficient estimates. In order to estimate them, the revenue shares for the relevant activities are used as a proxy for the amount of labour they require. Labour input for the different activities is then calculated based on these shares. The second procedure is due to the presence of infeasibilities in this model. In order to try and eliminate them, a number of courses of action can be followed from excluding outlying estimates to dropping regional estimates.
It should be noted that the reconciliation process has to be divided into these two steps because it is highly computationally burdensome. For the model to run properly (or even at all), it is necessary to divide it into two parts, with the one part obtaining plausible elements and the other implementing the final reconciliation.
Table 20: Total labour input coefficients from different econometric estimations and steps in reconciliation procedure (selected regions and crops)
| Region | crop or aggregate | Econometric estimation | HPD solution including | ||||
| regional | national- including yield | national - without yield | regional, national, crop aggregates | + expert assumption | + regional labour supply |
||
| Belgium (BL24) | Soft wheat | 31.49 | 31.26 | 31.49 | 24.99 | 32.73 | 53.88 |
| Sugar beet | 76.25 | 77.39 | 76.25 | 62.19 | 48.27 | 68.36 | |
| Cereals | 28.23 | 32.89 | 28.23 | 32.78 | 28.16 | 32.66 | |
| Root crops | 58.75 | 65.43 | 58.75 | 58.8 | 64.52 | 105.89 | |
| Germany (DEA1) | Soft wheat | 36.78 | 35.32 | 36.78 | 36.98 | 38.62 | 34.46 |
| Sugar beet | 82.01 | 58.99 | 82.01 | 55.06 | 39.61 | 43.58 | |
| Cereals | 40.13 | 32.63 | 40.13 | 39.94 | 41.65 | 35.12 | |
| Root crops | 28.83 | 14.23 | 28.83 | 38.32 | 41.26 | 0.01 | |
| France (FR24) | Soft wheat | 14.65 | 23.3 | 23.68 | 14.71 | 16.5 | 13.22 |
| Sugar beet | -7.42 | 2.24 | -1.68 | 11.08 | 19.72 | 18.5 | |
| Cereals | 10.48 | 35.9 | 22.7 | 15.61 | 15.43 | 12.7 | |
| Root crops | 11.68 | 29.78 | 19.42 | 17.05 | 24.64 | 18.43 | |
The Table visualizes the adjustments regarding an implausible labour input coefficient for sugar beet in a French region. The econometric estimation come up with very low or negative values. The HPD solution combining crop specific estimates with corresponding averages of crop aggregates corrects this untrustworthy value to 11.08 h/ha. This value is in an acceptable range but it strikes that in opposite to many other regions the labour input for sugar beet is still less than for soft wheat. After adding equations in the reconciliation procedure that ensure that the relation of labour input coefficients among crops follows an similar “European” pattern the labour input is supposed to be 19.72 h/ha. There is up to now no theoretical or empirical evidence for this similar pattern regarding relation of input coefficients but the results seem to be more plausible when checked with expert knowledge. In the last column bounds on regional labour supply derived from FADN are added which “scales” the regional value. This final result is and is now part of the CAPRI model.
Projecting Labour Use
For typical applications of CAPRI, regional projections of labour use are needed. Such projections have been prepared as well in the CAPSTRAT project, using a cohort analysis to separate 2 components of changes over time: (1) an autonomous component, which comprises structural changes due to demographic factors such as ageing, death, disability and early retirement, and (2) a non-autonomous component, which incorporates all other factors that influence changes in farm structure and has been analysed econometrically.
The results of this analysis are loaded in the context of CAPRI task “Generate trend projection” in file baseline\labour_ageline.gms, but only to serve as one type of bounds for labour use in the contrained trends for European regions. Other bounds are derived from engineering knowledge (or assumptions) on plausible labur use per activity which is based on the initial estimation of labour allocation by activity.