CAPRI Online Manual (update)

The term input allocation describes how aggregate input demand (e.g. total anorganic N fertiliser use in Denmark) is ‘distributed’ to production activities. The resulting activity specific data are called input coefficients. They may either be measured in value (€/ha) or physical terms (kg/ha). The CAPRI data base uses physical terms and, where not available, input coefficient measured in constant prices.

Micro-economic theory of a profit maximising producer requires revenue exhaustion, i.e. marginal revenues must be equal to marginal costs simultaneously for all realised activities. The marginal physical input demand multiplied with the input price exhausts marginal revenues, leading to zero marginal profits. Marginal input demands per activity can only be used to define aggregate input demand if they are equal to average input demands. The latter is the case for the Leontief production function.

The advantage of assuming a Leontief technology in agricultural production analysis is the fact that an explicit link between production activities and total physical input use is introduced (e.g. environmental indicators can be linked directly to individual activities or activity specific income indicators, since gross margins can be calculated). The disadvantage is the rather rigid technology assumption. We would for example expect that increasing a crop share in a region will change the average soil quality the crop uses, which in turn should change yields and nutrient requirements. It should hence be understood that the Leontief assumption is an abstraction and simplification of the ‘real’ agricultural technology in a region. The assumption is somewhat relaxed in CAPRI as two ‘production intensities’ are introduced.

Input coefficients for different inputs are constructed in different ways which will be discussed in more detail in the following sections:

• For nitrate, phosphate and potash, nutrient balances are constructed so to take into account crop and manure nutrient content and observed fertiliser use, combined with gaseous losses. These balances ex post determine the effective input coefficients and regional availability of manure and overfertilisation parameters.
• For feed, the input calculation is rooted in a mix of engineering knowledge (requirement functions for animal activities, nutrient content of feeding stuff, recommendations on feed mix), observed data ex post (total national feed use, national feed costs), combined within a Highest Posterior Density (HPD) estimation framework.
• For the remaining inputs, estimation results from a FADN sample in the context of the CAPSTRAT project (2000-03) are combined with current aggregate national input demand reported in the EAA and standard gross margin estimations, again using a HPD estimation framework.

There is a long history of allocating inputs to production activities in agricultural sector analysis, dating back to the days where I/O models and aggregate farm LPs where the only quantitative instruments available. In these models, the input coefficients represented a Leontief technology, which was put to work in the quantitative tools as well. However, input coefficients per activity do not necessary imply a Leontief technology. The allocated input demands can be seen as marginal ones (which are identical to average ones in the Leontief case) and are then compatible with flexible technologies as well.

Input coefficients can be put to work in a number of interesting fields. First of all, activity specific income indicators may be derived, which may facilitate analyzing results and may be used in turn to define sectoral income. Similarly, important environmental indicators are linked to input use and can hence be linked to activities as well with the help of input coefficients.

Given the importance or the input allocation, the CAP STRAT project (2000-2003) comprised an own work package to estimate input coefficients. On a first step, input coefficients were estimated using standard econometrics from single farm record as found in FADN. Additionally, tests for a more complex estimation framework building upon entropy techniques and integrating restrictions derived from cost minimization were run in parallel. The need to accommodate the estimation results with data from the EAA in order to ensure mutual compatibility between income indicators and input demand per activity and region on the one hand, and sectoral income indicators as well as sectoral input use on the other, requires deviating from the estimated mean of the coefficients estimated from single farm records. Further on, in some cases estimates revealed zero or negative input coefficients, which cannot be taken over. Accordingly, it was decided to set up a second stage estimation framework building upon the unrestricted estimates from FADN. The framework can be applied to years where no FADN data are available, and thus ensures that the results will be continuously used for the years ahead, before an update of the labor-intensive estimations is again necessary and feasible.

As a result of the unrestricted estimation based on FADN ¹⁾a matrix of input coefficients for 11 input categories (Total Inputs, Crop Only Inputs, Animal Only Inputs, Seeds, Plant Protection, Fertilizer, Other Crop Inputs, Purchased and Non-Purchased Feeds and Other Animal Only Inputs) and their estimated standard errors is available. Some of those coefficients are related to the output of a certain activity (e.g. how much money is spend on a certain input to produce one unit of a product), some of them are related to the acreage of on activity (input costs per activity level).

All of the econometric coefficients were required to be transformed into an ‘activity level’ form, due to the fact that this is the definition used in the CAPRI model. Before this could be done, it seemed necessary to fill up the matrix of estimated coefficients because some estimates were missing and others were negative. In order to this we constructed a number of coefficients that were weighted averages among certain groups. These mean coefficients were the following.

1. Mean coefficients of activity groups. Each activity was allocated to a certain group (e.g. soft wheat belonged to cereals). For each group we built weighted averages among the positive estimates within a group using the estimated t statistics as weights. This coefficient only existed if there was at least one positive estimate inside that group and was then used to replace the gaps inside the coefficient matrix. If that mean coefficient was not available, due to no positive estimate inside a group at all, the next type of mean coefficients became relevant:
2. Mean coefficients for an activity among European regions. This second type of mean coefficients calculates weighted averages among three types of regional clusters. These clusters are Northern European States, Southern European states and all European regions. Again, the estimated t statistics were used as aggregation weights. Unfortunately, this type of averages did not fill all gaps in the coefficient matrix as there were some activities that had no positive estimate over the entire EU. For those the third type of mean coefficients was calculated.
3. Mean coefficients for activity groups among regional clusters. Here we calculated for the three regional clusters the averages of the first type of mean coefficients. As even the latter are synthetic, we gave each mean of them the same weight. Fortunately there was only a small probability that this coefficient did not exist for one of the groups as this was only the case if no coefficient inside a group over the entire EU had a positive estimate, which was not the case.

Following these rules we finally got a matrix of estimated and synthetic calculated input coefficients for both, the ‘per activity level’ and the ‘per production’ unit definition²⁾. For the synthetic one there was no estimated standard error available but we wanted to use those later on. So we assumed them –to reflect that these coefficients have only weak foundation– to have a t statistic of 0.5.

The ‘per level’ definition was only taken over if the coefficient was really estimated or if no per production unit definition did exist. To transfer the latter into per activity level definition, we multiplied them with the average yield (1985 2001) of the respective activity. The resulting coefficients and their standard errors were then used a HPD approach as a first set of priors³⁾.

Missing econometric estimates and compatibility with EAA figures were not the only reasons that made a reconciliation of estimated inputs coefficients necessary. Moreover, the economic sense of the estimates could not be guaranteed and the definition of inputs in the estimation differed from the one used in CAPRI. Therefore we decided to include further prior information on input coefficients in agriculture. The second set of priors in the input reconciliation was therefore based on data from the EAA. Total costs of a certain input within an activity in a European Member State was calculated by multiplying the total expenditures on that input with the proportion of the total expected revenue of that activity to that of all activities using the input. Total expected revenue in this case was the production value (including market value and premiums) of the respective activity. If this resulted in a certain coefficient being calculated as zero due to missing data, then this coefficient would be replaced by one from a similar activity e.g. a zero coefficient for ‘MAIF’ would be replaced by the coefficient for ‘GRAS’

This kind of prior information tries to give the results a kind of economic sense. For the same reason the third type of priors was created based on standard gross margins for agricultural activities received from EUROSTAT. Those existed for nearly all activities. The set from 1994 was used, since this was the most complete available. Relative rather than absolute differences were important, given the requirement to conform to EAA values⁴⁾.

Given the three types of prior information explained above –estimated input coefficients, data from EAA and standard gross margins , a HPD estimator has been used to reconcile the prior information on input coefficients. Accounting constraints ensure (see in “dist_input.gms”) first that gross margins for an activity is the difference between expected revenue per activity level of that activity and the sum over all inputs used in that activity and second that the sum over all activities of their activity levels multiplied with an input gives the total expenditures on that input given by the EAA. The estimation is carried out in GAMS within and run for each year in the database. Some bounds are further set to avoid estimates running into implausible ranges.

The Highest Posterior Density estimation yields monetary input coefficients for the fertiliser types (Nitrate, Phosphate, Potassium), seeds, plant protection, feeds, pharmaceutical inputs, repairs, agricultural service input, energy and other inputs. While some of these can be directly used in the CAPRI model, we need special treatments for others –e.g. fertilisers, because they are used in physical units inside the model, and feeds, since they are much more disaggregated.

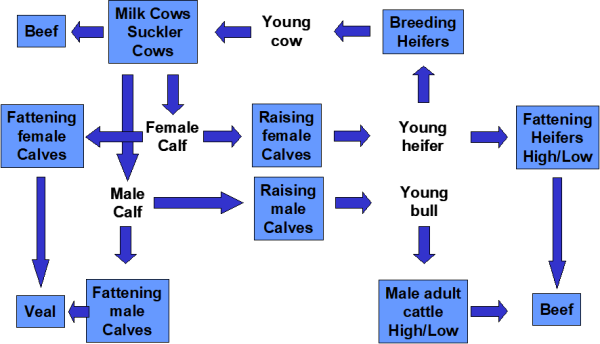
Figure below shows the different cattle activities and the related young animal products used in the model. Milk cows (DCOL, DCOH) and suckler cows (SCOW) produce male and female calves (YCAM, YCAF). The relation between male and female calves is estimated ex post in the COCO framework. These calves are assumed to weigh 50 kg at birth (see gams\feed\feed_decl.gms) and to be born on the 1st of January. They enter immediately the raising processes for male and female calves (CAMR, CAFR) which produce young heifers (YHEI, 300 kg live weight) and young bulls (YBUL, 335 kg). The raising processing are assumed to take one year, so that calves born in t enter the processes for male adult fattening (BULL, BULH), heifers fattening (HEIL, HEIH) or heifers raising (HEIR) on the 1st January of the next year t+1. The heifers raising process produces then the young cows which can be used for replacement or herd size increasing on the first of January of t+2. The table below the diagram shows a numerical example (for DK, 1999-2001) for these relationships.

Figure 5. The cattle chain