Welfare analysis
A key element in analysing policy changes from an economic viewpoint is to look at welfare changes. The “classical” elements of a welfare analysis are changes in consumer and producer rents and for the tax payer. That concept is also followed in CAPRI.
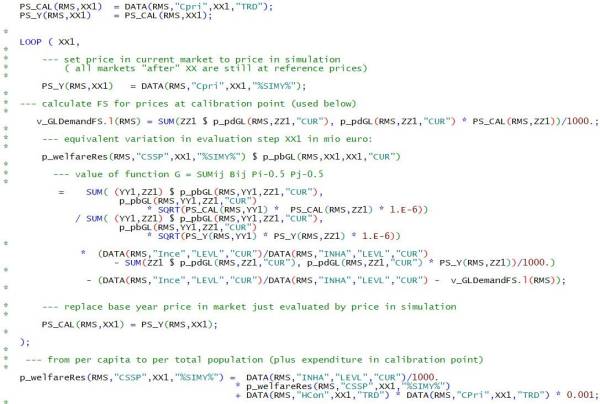
For consumers, CAPRI uses the money metric concept. It can be broadly understood as a measurement for changes in the purchasing power of the consumer. The concept is also linked to the expenditure function as introduced in Section Behavioural equations for final demand:
\begin{equation} M(cpri^r,cpri^s,Y^r )=e(cpri^r,U(cpri^s,Y^r )) \end{equation}
Where e(.) is the expenditure function, \(Y^r\) is expenditure in the reference situation, and \(cpri^r (cpri^s)\) is the price vector in the reference (scenario) situation. The money metric is thus the expenditure the consumer would need at reference prices to be as well of as if facing the scenario prices at reference income. The difference of money metric for a given scenario to money metric in the reference situation is the equivalent variation. Considering the generalised Leontief form of the indirect utility function used in CAPRI (compare with Section Behavioural equations for final demand) we get
\begin{align} \begin{split} e (cpri^r, U(cpri^s,Y^r)) &= \left\{ F^r+ \frac{G^r}{G^s⁄(Y^r-F^s)}-Y^r \right\}+Y^r \\ & = \left\{ \frac {G^r}{G^s}(Y^r-F^s )-(Y^r-F^r ) \right\}+Y^r \end{split} \end{align}
The bracket {} is the equivalent variation of the change from the reference to the scenario situation. In the code (in gams\reports\welfare.gms) the momey metric is computed in a loop over products such that the contributions of single products are displayed1). It is also considered that the per capita demand needs to be multiplied with population.
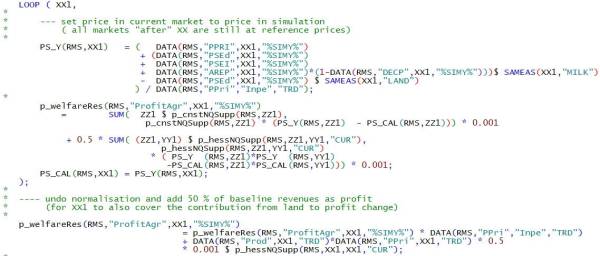
For some agents the welfare accounting involves particularities for those regions covered by the regional programming models that will be discussed below. In the general case (for “non supply model regions”) producer welfare may be derived in the market model from the normalised profit function underlying the supply functions and the input demands for feed energy and land:
\begin{equation} \pi(p^s)=π_0+\sum_x as_x p_x^s+0.5 \sum_{x,y} bs_{x,y} p_x^s p_y^s \end{equation}
where \(p^s\) is the price vector in the scenario situation and the arbitrary constant \(\pi_0\) has been chosen as 50% of reference run revenues. In order to show the changes in producer welfare by product we compute producer welfare in the scenario as follows:
\begin{equation} \pi(p^s)-\pi(p^r)+\pi_0=\sum_x as_x(p_x^s-p_x^r)+0.5\sum_{x,y}bs_{x,y}(p_x^s p_y^s - p_x^r p_y^r )+\pi_0 \end{equation}
In the code (in gams\reports\welfare.gms) we are also considering that it is necessary to revert the normalisaiton of prices with the general price index
CAPRI uses the normalised quadratic form also for other agents, such that the calculation of welfare changes is very similar for
- the dairy industry (with margins adopting the role of prices)
- the processing industry (again with margins adopting the role of prices)
- the feed industry
Land supply is currently specified as responding to the log of land rents according to a land supply elasticity which also permits an easy calculation of land owner rent.
In the global market model, the main effects on taxpayer welfare comes through tariff revenues. Here it is also necessary to consider the allocation of TRQ rents, and if several bahavioural (“RMS”) regions are combined into a single market region (“RM”) then the tariff revenues of the market region need to be allocated.
For European (supply model) regions there are a number of particularities. First of all, CAPRI uses changes in the gross value added (GVA) plus premiums as the main indicator of producer (farmer) welfare. The gross value added is the difference between revenues (output quantities valued at farm gate prices) and intermediate input costs (input quantities with the exemption of the primary factors land, capital and labour multiplied with their farm gate prices). The GVA plus premiums is hence the sum the farming sector can spend to remunerate labour, capital and land, independent of property rights of these factors. GVA including subsidies is a traditional measure of “farm income” which has been one of the most important objectives of the CAP in the early years of CAPRI. It was considered useful therefore to monitor farm income defined in this way in the database and to compute it for scenarios. GVA plus premiums differs from some other income indicators
- “Farm profits” may be computed from GVA plus premiums considering ownership and some accounting rules for depreciation of capital, and family as well as non-family labour costs.
- “Economic profit” in the sence of the supply models would be the value of the supply model objective function which depends critically on the specification of unobserved cost function parameters (PMP).
- Farm household income would also consider non-farm income sources and income of all household members and therefore clearly differs from GVA.
Due to the allocation of output and input to individual activities, CAPRI allows to calculate the GVA for single production activities, and to aggregate it from there to groups of activities and over regions.
“Land owner welfare” and “feed industry welfare” are also treated differently as compared to non-European regions, in line with the supply model specification for land supply and feed use. Regarding “land owner welfare” the supply models specify costs for the supply of land to farming that may be interpreted as the opportunity costs of non-agricultural land use. Deducting this opportunity cost of land ensures that scenarios involving changes in land supply are not assessed in a biased way (e.g. by treating land as a “free” input without a price).
Feed demand is also reflected already in the supply models, in fact in a quite sophisticated manner, which balances not only for feed energy (as in the global market model) but also for protein. The GVA plus premiums therefore already includes the effects of changing feed costs and no additional calculation is needed.
The final particularity derives from the detailed representation of the CAP premium system in the supply models. For premium schemes, financing rates for the EU and national budgets as well as for pillar I and II of the CAP are defined, which allow to allocate costs to those different budgets. A few other CAP instruments have become largely irrelevant in the meantime, like the cost of public market “interventions” (purchases for storage at public cost), export subsidization and some subsidies paid for demanders of agricultural goods. These are also covered in the CAPRI welfare accounting (in case they would be revitalised).