The CAPRI global market model is a spatial comparative static Multi-Commodity model. It covers 47 primary and secondary agricultural products. Product quantities are expressed in physical primary product equivalent according to the concept of Supply Utilization Accounts of FAO. The global market is a square system of equations without an objective function. Its equations may be interpreted as the first order conditions from simultaneously maximizing globally producers' and consumer's rents in competitive international agricultural markets at given non-agricultural prices (primary factors, agricultural inputs and any other produces) and income.

It is spatial by which is meant that bi-lateral trade flows are included in the model. As the number of non-zero trade flows matrices tend to increase quadratically with the number of country blocks in a spatial model, not all countries of the world are covered individually. Rather, CAPRI uses 32 trade blocks, leading to a total of around 46.000 endogenous variables and the same number of equations. Some of the trade blocks, as EU15 or EU10 are broken down to individual countries to allow for a welfare analysis at the country level so that the model differentiates between 67 individual countries or country blocks. Changes in the trade flows are based on the Armington assumption which uses a CES utility function to aggregate from single trade flows to total market appearances so that trade shares depend on price relations. Two CES nests are applied: one to break total market appearances into from domestic production and imports, and a second one to break imports into individual origins. Accordingly, it is assumed that product quality is differentiated by origin and determines the willingness to pay of the consumer.

Import prices are derived from domestic prices of the exporter by adding fixed per unit transport costs and ad-valorem and specific tariffs, and where applicable, by subtracting export subsidies. Some of the tariffs are differentiated by origin to capture bi-lateral trade agreements or preferences, and some are endogenous when depending on Tariff Rate Quotas (TRQs). CAPRI differentiates between global TRQs where the import tariffs of all importers depends on total imports, and bi-lateral TRQs where import prices of a specific importer depend on the specific trade flow. Exporters first fill their bi-laterally assigned TRQs before they export into global ones. Equally, so-called flexible levies for cereals and minimum import prices for fruits and vegetables are included, again leading to endogenous tariffs.

Intervention purchases are modelled based on the probablity density of EU domestic market prices to undercut administrative ones, taking into account maximal intervention quantities.

The market model is based on a strict template approach. The market for each commodity and region is modelled by structurally identical equations, differences are expressed by regional and commodity specific parameters describing behaviour, technology and policy instruments. That allowed in the past an expansion to new products and an increased regional break-down when data availability and computing power increased.

The market part of CAPRI is based on functional forms which ensure globally symmetry, homogeniety and correct curvature. The functions are second order flexible which means that can be calibrated against any set of own and cross-price elasticities which are in line with micro-economic conditions at the prices and quantities of the calibration point. For ex-ante simulations, the calibration is performed at the future prices and quantities of the baseline.

That ease the integations of results from econometric studies or mimicking the behaviour of other models in CAPRI. Recently, to give an example, price sensitivitiy experiments with the highly detailed agricultural sector model SILAS from Switzerland were used to derive the parameterisation of the related behavioural equations in CAPRI.

Supply, feed and processing demand are modelled based on a normalized quadratic profit function. A fudging function ensure that only positive values are returned. The normalization is based on a price index which captures the price of all non-agricultual products. The calibration of the parameters includes a Cholesky-Decomposition to ensure that the parameter matrix is strictly definite to ensure the convexity of the solution space. Processing demand is driven by processing margins.

Human consumption is modelled based on a generalized Leontief expenditure function.

The bi-lateral trade flows are based on FAOSTAT, as are the items of the market balances (production, feed demand, processing demand, human consumption) for the countries not covered by the supply part.

Most favourite nation tariffs and data for some of the TRQs stem from the AMAD data base. Data on further TRQs and on bi-lateral agreements are taken from EU legislation, which is also used to determine the flexible levies and the import regimes for fruits and vegetables.

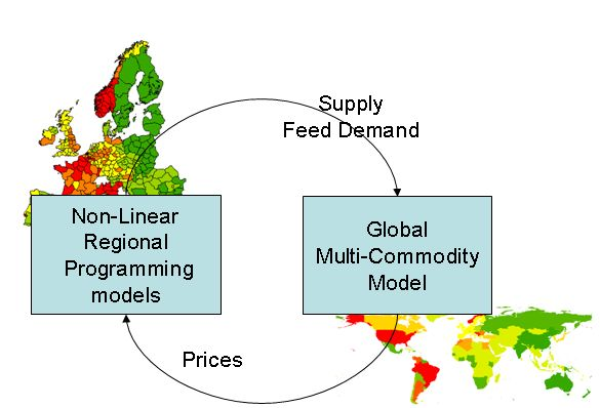
In order to link the supply and the market model, the behavioural parameters for supply and feed demand for the countries covered by the supply part are sequentially updated to the results of the supply part.

As the rest of the CAPRI modelling system, the market model is realised in GAMS. The non-linear solver CONOPT developed by Arne Drud is used to solve it. The CAPRI teams wants to thank Arne Drud for his support and continous improvements to CONOPT over the years which were indispensable for that kind of large-scale modelling work. In order to allow for a speedily solution, the model may be broken down to individual products or products groups solved at fixed cross-prices before the full model is attacked. Typcially, once a feasible solution was found, new instances in the iterative solution procedures can be solved around 10 seconds.